pacman::p_load(tmap, sf, tidyverse, sfdep, knitr, Hmisc, mapview, DT)Take-home 1 - Geospatial Analytics for Public Goods

1 Overview
As cities upgrade to digital systems, like smart buses and GPS, a lot of data is created about how people move around. This data is super useful for understanding patterns in both space (where) and time (when). For example, on public buses, smart cards and GPS devices collect information about routes and how many people are riding. This data holds clues about how people behave in the city, and understanding these patterns can help manage the city better and give an edge to transportation providers.
But, often, this valuable data is only used for basic things like tracking and mapping using Geographic Information System (GIS) applications. This is because regular GIS tools struggle to fully analyze and model this kind of complex spatial and time-related data.
In this exercise, we’re going to focus on bus trips during specific peak hours:
| Peak hour period | Bus tap on time |
|---|---|
| Weekday morning peak | 6am to 9am |
| Weekday afternoon peak | 5pm to 8pm |
| Weekend/holiday morning peak | 11am to 2pm |
| Weekend/holiday evening peak | 4pm to 7pm |
To better understand these movement patterns and behaviors, we’re going to use something called Exploratory Spatial Data Analysis (ESDA). It’s like a powerful tool that helps us tackle complex challenges in society. In this project, we’re going to use specific methods Local Indicators of Spatial Association (LISA) that will help us dig deep into the data and uncover valuable insights.
Local Indicators of Spatial Association (LISA) statistics serve two primary purposes. Firstly, they act as indicators of local pockets of nonstationarity, or hotspots. Secondly, they are used to assess the influence of individual locations on the magnitude of a global statistic. In simpler terms, LISA helps in identifying specific areas (like hotspots) that differ significantly from their surrounding areas and evaluates how these individual areas contribute to the overall pattern observed in a larger region.
the content of the following panel explained what aspatial and geospatial data are used in this project.
Monthly Passenger Volume by Origin Destination Bus Stops:
August, September and October 2023 Period
downloaded from LTA DataMall - Dynamic Dataset via API
csvformat.Columns/Fields in the dataset includes YEAR_MONTH, DAY_TYPE, TIME_PER_HOUR, PT_TYPE, ORIGIN_PT_CODE, DESTINATION_PT_CODE, and TOTAL_TRIPS.
Two geospatial data in shp format are used in this project, which includes:
Bus Stop Location from LTA DataMall - Static Dataset. It provides information about all the bus stops currently being serviced by buses, including the bus stop code (identifier) and location coordinates.
hexagon, a hexagon layer of 500m (perpendicular distance between the centre of the hexagon and its edges.) Each spatial unit is regular in shape and finer than the Master Plan 2019 Planning Sub-zone GIS data set of URA.
Uniform Distances Everywhere: Think of hexagons as honeycomb cells. Each cell (hexagon) touches its neighbors at the same distance from its center. It’s like standing in the middle of a room and being the same distance from every wall, making it easier to measure and compare things.
Outlier-Free Shape: Hexagons are like well-rounded polygons without any pointy tips. Sharp corners can create odd spots in data, but hexagons smoothly cover space without sticking out anywhere. This helps prevent weird data spikes that don’t fit the pattern.
Consistent Spatial Relationships: Imagine a beehive where every hexagon is surrounded by others in the same pattern. This regular pattern is great for analyzing data because you can expect the same relationships everywhere, making the data predictable and easier to work with.
Ideal for Non-Perpendicular Features: Real-world features like rivers and roads twist and turn. Squares can be awkward for mapping these, but hexagons, which are more circular, can follow their flow better. This way, a hexagon-based map can mimic the real world more closely than a checkerboard of squares.
Summarized from: Dhuri, and Sekste & Kazakov.
2 Preparation
Before starting with the analysis, we have to load the library (and install it if it does not exist in the environment yet) and import the data. This section also contains minor checking and setup of the data.
2.1 Import Library
Explanations for the imported library:
tmap for visualizing geospatial
sf for handling geospatial data
tidyverse for handling aspatial data
sfdep for computing spatial weights, global and local spatial autocorrelation statistics, and
knitr for creating html tables
Hmisc for summary statistics
mapview for interactive map backgrouds
DT library to create interactive html tables
2.2 Import and Setup the Data
The following section will import the required aspatial and geospatial dataset.
Aspatial
the following code will import all the origin destination bus data and show the summary statistics of the dataset. The process involved:
import the csv file using
read_csvfunction from readr packageusing mutate from dplyr package, transform georeference data type into factors for easing compatibility issue and more efficient processing.
using describe from hmisc package, display the summary statistics of the dataset.
Code
# Load each csv file
odb8 <- read_csv("../data/aspatial/origin_destination_bus_202308.csv.gz")
# change georeference data type into factors
odb8 <- odb8 %>%
mutate(
ORIGIN_PT_CODE = as.factor(ORIGIN_PT_CODE),
DESTINATION_PT_CODE = as.factor(DESTINATION_PT_CODE)
)
# check the dataframe
describe(odb8)odb8
7 Variables 5709512 Observations
--------------------------------------------------------------------------------
YEAR_MONTH
n missing distinct value
5709512 0 1 2023-08
Value 2023-08
Frequency 5709512
Proportion 1
--------------------------------------------------------------------------------
DAY_TYPE
n missing distinct
5709512 0 2
Value WEEKDAY WEEKENDS/HOLIDAY
Frequency 3279836 2429676
Proportion 0.574 0.426
--------------------------------------------------------------------------------
TIME_PER_HOUR
n missing distinct Info Mean Gmd .05 .10
5709512 0 24 0.997 14.07 5.949 6 7
.25 .50 .75 .90 .95
10 14 18 21 22
lowest : 0 1 2 3 4, highest: 19 20 21 22 23
--------------------------------------------------------------------------------
PT_TYPE
n missing distinct value
5709512 0 1 BUS
Value BUS
Frequency 5709512
Proportion 1
--------------------------------------------------------------------------------
ORIGIN_PT_CODE
n missing distinct
5709512 0 5067
lowest : 01012 01013 01019 01029 01039, highest: 99139 99161 99171 99181 99189
--------------------------------------------------------------------------------
DESTINATION_PT_CODE
n missing distinct
5709512 0 5071
lowest : 01012 01013 01019 01029 01039, highest: 99139 99161 99171 99181 99189
--------------------------------------------------------------------------------
TOTAL_TRIPS
n missing distinct Info Mean Gmd .05 .10
5709512 0 3544 0.982 21.04 33.59 1 1
.25 .50 .75 .90 .95
2 4 13 38 74
lowest : 1 2 3 4 5, highest: 30799 31669 32508 33424 35049
--------------------------------------------------------------------------------Code
# Load each csv file
odb9 <- read_csv("../data/aspatial/origin_destination_bus_202309.csv.gz")
# change georeference data type into factors
odb9 <- odb9 %>%
mutate(
ORIGIN_PT_CODE = as.factor(ORIGIN_PT_CODE),
DESTINATION_PT_CODE = as.factor(DESTINATION_PT_CODE)
)
# check the dataframe
describe(odb9)odb9
7 Variables 5714196 Observations
--------------------------------------------------------------------------------
YEAR_MONTH
n missing distinct value
5714196 0 1 2023-09
Value 2023-09
Frequency 5714196
Proportion 1
--------------------------------------------------------------------------------
DAY_TYPE
n missing distinct
5714196 0 2
Value WEEKDAY WEEKENDS/HOLIDAY
Frequency 3183300 2530896
Proportion 0.557 0.443
--------------------------------------------------------------------------------
TIME_PER_HOUR
n missing distinct Info Mean Gmd .05 .10
5714196 0 23 0.997 14.06 5.94 6 7
.25 .50 .75 .90 .95
10 14 18 21 22
lowest : 0 1 2 4 5, highest: 19 20 21 22 23
--------------------------------------------------------------------------------
PT_TYPE
n missing distinct value
5714196 0 1 BUS
Value BUS
Frequency 5714196
Proportion 1
--------------------------------------------------------------------------------
ORIGIN_PT_CODE
n missing distinct
5714196 0 5067
lowest : 01012 01013 01019 01029 01039, highest: 99139 99161 99171 99181 99189
--------------------------------------------------------------------------------
DESTINATION_PT_CODE
n missing distinct
5714196 0 5072
lowest : 01012 01013 01019 01029 01039, highest: 99139 99161 99171 99181 99189
--------------------------------------------------------------------------------
TOTAL_TRIPS
n missing distinct Info Mean Gmd .05 .10
5714196 0 3274 0.981 19.59 31.01 1 1
.25 .50 .75 .90 .95
2 4 12 35 69
lowest : 1 2 3 4 5, highest: 27356 28248 28510 30096 31674
--------------------------------------------------------------------------------Code
# Load each csv file
odb10 <- read_csv("../data/aspatial/origin_destination_bus_202310.csv.gz")
# change georeference data type into factors
odb10 <- odb10 %>%
mutate(
ORIGIN_PT_CODE = as.factor(ORIGIN_PT_CODE),
DESTINATION_PT_CODE = as.factor(DESTINATION_PT_CODE)
)
# check the dataframe
describe(odb10)odb10
7 Variables 5694297 Observations
--------------------------------------------------------------------------------
YEAR_MONTH
n missing distinct value
5694297 0 1 2023-10
Value 2023-10
Frequency 5694297
Proportion 1
--------------------------------------------------------------------------------
DAY_TYPE
n missing distinct
5694297 0 2
Value WEEKDAY WEEKENDS/HOLIDAY
Frequency 3259419 2434878
Proportion 0.572 0.428
--------------------------------------------------------------------------------
TIME_PER_HOUR
n missing distinct Info Mean Gmd .05 .10
5694297 0 23 0.997 14.04 5.933 6 7
.25 .50 .75 .90 .95
10 14 18 21 22
lowest : 0 1 2 4 5, highest: 19 20 21 22 23
--------------------------------------------------------------------------------
PT_TYPE
n missing distinct value
5694297 0 1 BUS
Value BUS
Frequency 5694297
Proportion 1
--------------------------------------------------------------------------------
ORIGIN_PT_CODE
n missing distinct
5694297 0 5073
lowest : 01012 01013 01019 01029 01039, highest: 99139 99161 99171 99181 99189
--------------------------------------------------------------------------------
DESTINATION_PT_CODE
n missing distinct
5694297 0 5077
lowest : 01012 01013 01019 01029 01039, highest: 99139 99161 99171 99181 99189
--------------------------------------------------------------------------------
TOTAL_TRIPS
n missing distinct Info Mean Gmd .05 .10
5694297 0 3495 0.982 20.76 33.13 1 1
.25 .50 .75 .90 .95
2 4 12 37 73
lowest : 1 2 3 4 5, highest: 30985 31349 32355 35931 36668
--------------------------------------------------------------------------------Explanations for each field in the data can be found in the following metadata.
YEAR_MONTH: Represent year and Month in which the data is collected. Since it is a monthly data frame, only one unique value exist in each data frame.
DAY_TYPE: Represent type of the day which classified as weekdays or weekends/holidays.
TIME_PER_HOUR: Hour which the passenger trip is based on, in intervals from 0 to 23 hours.
PT_TYPE: Type of public transport, Since it is bus data sets, only one unique value exist in each data frame (i.e. bus)
ORIGIN_PT_CODE: ID of origin bus stop
DESTINATION_PT_CODE: ID of destination bus stop
TOTAL_TRIPS: Number of trips which represent passenger volumes
Geospatial
the following panel show the import process for the bus stop geospatial data. The geospatial layer of the data shows point location of bus stops across Singapore.
The geospatial data is imported using st_read function from sf package. As previously done, while reading the data, categorical data that can serve as reference are converted into factors for easing compatibility issue and more efficient processing. The imported dataset is then checked using glimpse function from dplyr package that shows the columns, a glimpse of the values and the data type.
busstop <- st_read(
dsn = "../data/geospatial",
layer = "BusStop"
) %>%
mutate(
BUS_STOP_N = as.factor(BUS_STOP_N),
BUS_ROOF_N = as.factor(BUS_ROOF_N),
LOC_DESC = as.factor(LOC_DESC)
)Reading layer `BusStop' from data source `C:\ameernoor\ISSS624\data\geospatial' using driver `ESRI Shapefile'
Simple feature collection with 5159 features and 3 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 3970.122 ymin: 26482.1 xmax: 48280.78 ymax: 52983.82
Projected CRS: SVY21# check the output
glimpse(busstop)Rows: 5,159
Columns: 4
$ BUS_STOP_N <fct> 22069, 32071, 44331, 96081, 11561, 66191, 23389, 54411, 285…
$ BUS_ROOF_N <fct> B06, B23, B01, B05, B05, B03, B02A, B02, B09, B01, B16, B02…
$ LOC_DESC <fct> OPP CEVA LOGISTICS, AFT TRACK 13, BLK 239, GRACE INDEPENDEN…
$ geometry <POINT [m]> POINT (13576.31 32883.65), POINT (13228.59 44206.38),…Check the unique values
To see more of the data characteristics, the following panel will show the number of distinct values in each column. it use n_distinct function from dplyr package.
count of unique/distinct values are:
Code
n_distinct(busstop$BUS_STOP_N)[1] 5144count of unique/distinct values are:
Code
n_distinct(busstop$BUS_ROOF_N)[1] 97count of unique/distinct values are:
Code
n_distinct(busstop$LOC_DESC)[1] 4554count of unique/distinct values are:
Code
n_distinct(busstop$geometry)[1] 5158Explanations for each field in the data can be found in the following metadata.
- BUS_STOP_N: The unique identifier for each bus stop.
- BUS_ROOF_N: The identifier for the bus route or roof associated with the bus stop.
- LOC_DESC: Location description providing additional information about the bus stop’s surroundings.
- geometry: The spatial information representing the location of each bus stop as a point in the SVY21 projected coordinate reference system.
To ensure that geospatial data from different sources can be processed together, both have to be projected using similar coordinate systems and be assigned the correct EPSG code based on CRS. The st_crs function is used to check for ESPG Code and Coordinate System of both geospatial files. For Singapore, the coordinate system is SVY21 with EPSG 3414 (source: epsg.io). The following code chunk output shows how the CRS was initially not 3414, then corrected using st_set_crs. Both function are from sf package. Simultaneously, the dataframe is also prepared for joining process. It involve standardization of the data type to factor and using tolower function from base R package.
Code
# Check the current Coordinate Reference System (CRS) of the busstop dataset
print(st_crs(busstop))Coordinate Reference System:
User input: SVY21
wkt:
PROJCRS["SVY21",
BASEGEOGCRS["WGS 84",
DATUM["World Geodetic System 1984",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]],
ID["EPSG",6326]],
PRIMEM["Greenwich",0,
ANGLEUNIT["Degree",0.0174532925199433]]],
CONVERSION["unnamed",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["Degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["Degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["(E)",east,
ORDER[1],
LENGTHUNIT["metre",1,
ID["EPSG",9001]]],
AXIS["(N)",north,
ORDER[2],
LENGTHUNIT["metre",1,
ID["EPSG",9001]]]]# Assign a new EPSG code (Spatial Reference ID)
busstop <- st_set_crs(
busstop,
3414
) %>%
# Rename the bus stop origin column for easier joining with the main dataframe
mutate(
ORIGIN_PT_CODE = as.factor(BUS_STOP_N)
) %>%
select(
ORIGIN_PT_CODE,
LOC_DESC,
geometry
) %>%
# Change all column names to lowercase for consistency
rename_with(
tolower, everything()
)Code
print(st_crs(busstop))Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]3 Data Wrangling
Following the initial preparation, this section will do further data checking and processing before the analysis.
3.1 Check for Duplicates
In this step, we inspect the dataset for duplicate entries. This precautionary step is crucial to avoid the inadvertent repetition of records, which could lead to the overcounting of passenger trips. By identifying and addressing duplicates at this stage, we ensure the accuracy and reliability of our analysis, laying the groundwork for more precise and trustworthy results in the subsequent analytical processes. Checking for duplicates is a fundamental practice that contributes to the integrity of the data and the overall robustness of the geospatial analysis.
the following code is used to check duplicates and show how many duplicates exist in each odb.
Code
# Count the number of rows in each dataframe with duplicates
count_duplicate_rows <- function(df, df_name) {
df %>%
group_by_all() %>%
filter(n() > 1) %>%
ungroup() %>%
summarise(df_name = df_name, row_count = n())
}
# Apply the function to each dataframe
duplicate1 <- count_duplicate_rows(odb8, "odb8")
duplicate2 <- count_duplicate_rows(odb9, "odb9")
duplicate3 <- count_duplicate_rows(odb10, "odb10")
# Combine the results
all_duplicates <- bind_rows(duplicate1, duplicate2, duplicate3)
# Print the counts
print(all_duplicates)# A tibble: 3 × 2
df_name row_count
<chr> <int>
1 odb8 0
2 odb9 0
3 odb10 0- group_by_all from dplyr package to group a data frame by all of its variables. Essentially, it creates groups based on every column present in the data frame.
- filter from dplyr package to subset a data frame, retaining all rows that satisfy your conditions. To be retained, the row must produce a value of TRUE for all conditions.
- ungroup from dplyr package to remove grouping information from a data frame. When you have a grouped data frame (created using functions like group_by), ungroup will return it to its original, ungrouped state. This is useful when you’ve finished performing grouped operations (like summarization) and want to perform operations that don’t require the data to be grouped, or to prevent accidental misinterpretation or errors in subsequent data manipulations that are not intended to be group-wise operations.
- filter from dplyr package to subset a data frame, retaining all rows that satisfy your conditions. To be retained, the row must produce a value of TRUE for all conditions.
- summarise from sf package used to compute summary statistics or aggregate values for groups of data. When used on spatial data frames (such as those handled by sf), summarise can perform operations like calculating the mean, maximum, or sum of a particular variable for each group. This function is often used in combination with group_by to define the groups for which the summary statistics will be calculated. The result is a simplified representation of the data, focusing on key aggregated metrics.
- bind_rows from dplyr package to to combine two or more data frames by rows. It stacks the data frames on top of each other, effectively appending the rows of the second data frame to the first, the third to the combined first and second, and so on. This function is particularly useful when you have multiple data frames with the same variables and you want to create a single, combined data frame. It’s important that the columns in the data frames are compatible, either having the same names and types, or being able to be coerced into the same type.
The result shows that there are no duplicated data in the origin destination bus dataset. Note that the checking was based on a very loose criteria of duplicate, in which duplicated rows need to have the same value across all columns.
the following code is used to check duplicates and show how many duplicates exist in bus stop dataset and display the result.
Code
# Subset rows where origin_pt_code has duplicates
duplicates <- busstop[duplicated(busstop$origin_pt_code) | duplicated(busstop$origin_pt_code, fromLast = TRUE), ]
# Display the rows with duplicate origin_pt_code
kable(head(duplicates, n=32))| origin_pt_code | loc_desc | geometry | |
|---|---|---|---|
| 149 | 58031 | OPP CANBERRA DR | POINT (27089.69 47570.9) |
| 166 | 62251 | Bef Blk 471B | POINT (35500.54 39943.41) |
| 229 | 51071 | MACRITCHIE RESERVOIR | POINT (28300.11 36045.9) |
| 280 | 47201 | NA | POINT (22616.75 47793.68) |
| 341 | 58031 | OPP CANBERRA DR | POINT (27111.07 47517.77) |
| 512 | 22501 | Blk 662A | POINT (13489.09 35536.4) |
| 765 | 82221 | BLK 3A | POINT (35323.6 33257.05) |
| 1359 | 68091 | AFT BAKER ST | POINT (32164.11 42695.98) |
| 1527 | 51071 | MACRITCHIE RESERVOIR | POINT (28305.37 36036.67) |
| 1660 | 43709 | BLK 644 | POINT (18963.42 36762.8) |
| 1995 | 97079 | OPP ST. JOHN’S CRES | POINT (44144.57 38980.25) |
| 2093 | 82221 | Blk 3A | POINT (35308.74 33335.17) |
| 2096 | 97079 | OPP ST. JOHN’S CRES | POINT (44055.75 38908.5) |
| 2150 | 22501 | BLK 662A | POINT (13488.02 35537.88) |
| 2296 | 62251 | BEF BLK 471B | POINT (35500.36 39943.34) |
| 2724 | 68099 | BEF BAKER ST | POINT (32154.9 42742.82) |
| 2843 | 52059 | OPP BLK 65 | POINT (30770.3 34460.06) |
| 3044 | 67421 | CHENG LIM STN EXIT B | POINT (34548.54 42052.15) |
| 3189 | 53041 | Upp Thomson Road | POINT (28105.8 37246.76) |
| 3193 | 53041 | Upp Thomson Road | POINT (27956.34 37379.29) |
| 3260 | 77329 | BEF PASIR RIS ST 53 | POINT (40765.35 39452.18) |
| 3266 | 77329 | Pasir Ris Central | POINT (40728.15 39438.15) |
| 3269 | 96319 | Yusen Logistics | POINT (42187.23 34995.78) |
| 3270 | 96319 | YUSEN LOGISTICS | POINT (42187.23 34995.78) |
| 3296 | 52059 | BLK 219 | POINT (30565.45 36133.15) |
| 3371 | 43709 | BLK 644 | POINT (18952.02 36751.83) |
| 3697 | 68091 | AFT BAKER ST | POINT (32038.84 43298.68) |
| 3698 | 68099 | BEF BAKER ST | POINT (32004.05 43320.34) |
| 4590 | 47201 | W’LANDS NTH STN | POINT (22632.92 47934) |
| 5074 | 67421 | CHENG LIM STN EXIT B | POINT (34741.77 42004.21) |
- duplicated from the base R package is used to identify duplicate elements in a vector or rows in a data frame. It returns a logical vector indicating which elements or rows are duplicates of elements or rows with smaller indices.
- kable from the knitr package creates simple tables from a data frame, matrix, or other table-like structures. The function provides a user-friendly way to display tables in a markdown format.
The result shows that there are some duplicated data in the geospatial bus stop dataset. This might interfere with the joining data process and generated double count on later on. Note that the checking was based on the origin_pt_code field only, because it will be the basis of reference for joining the dataset later on. At a glance, the table above also show that, the duplicated code are actually located near each other. Therefore, removing the duplicates can be considered safe as the remaining bus stop code can represent the deleted one.
The folowing code chunk will execute the duplicate removal and show the result where number of rows have reduced from 5161 to 5145.
Code
# Keep one row of the duplicates in the original dataset
busstop <- busstop[!duplicated(busstop$origin_pt_code) | duplicated(busstop$origin_pt_code, fromLast = TRUE), ]
# Display the resulting dataset
glimpse(busstop)Rows: 5,144
Columns: 3
$ origin_pt_code <fct> 22069, 32071, 44331, 96081, 11561, 66191, 23389, 54411,…
$ loc_desc <fct> OPP CEVA LOGISTICS, AFT TRACK 13, BLK 239, GRACE INDEPE…
$ geometry <POINT [m]> POINT (13576.31 32883.65), POINT (13228.59 44206.…3.2 Categorical Peak Time Variable
on the interest of analyzing the peak time, the following code will assign new column that categorize peak time, filter data that is not on peak time, and show a sample of the output.
Code
# Function to categorize and aggregate trips
categorize_and_aggregate <- function(odb) {
odb <- odb %>%
# Categorize trips under periods based on day and timeframe
mutate(period = case_when(
DAY_TYPE == "WEEKDAY" & TIME_PER_HOUR >= 6 & TIME_PER_HOUR <= 9 ~ "Weekday morning peak",
DAY_TYPE == "WEEKDAY" & TIME_PER_HOUR >= 17 & TIME_PER_HOUR <= 20 ~ "Weekday evening peak",
DAY_TYPE == "WEEKENDS/HOLIDAY" & TIME_PER_HOUR >= 11 & TIME_PER_HOUR <= 14 ~ "Weekend/holiday morning peak",
DAY_TYPE == "WEEKENDS/HOLIDAY" & TIME_PER_HOUR >= 16 & TIME_PER_HOUR <= 19 ~ "Weekend/holiday evening peak",
TRUE ~ "non-peak"
)) %>%
# Only retain needed periods for analysis
filter(period != "non-peak") %>%
# Compute the number of trips per origin bus stop per month for each period
group_by(YEAR_MONTH, period, ORIGIN_PT_CODE) %>%
summarise(num_trips = sum(TOTAL_TRIPS)) %>%
# Change all column names to lowercase
rename_with(tolower, everything()) %>%
ungroup()
return(odb)
}
# Apply the function to each dataset
odb8 <- categorize_and_aggregate(odb8)
odb9 <- categorize_and_aggregate(odb9)
odb10 <- categorize_and_aggregate(odb10)
# sample the result
glimpse(odb10)Rows: 20,072
Columns: 4
$ year_month <chr> "2023-10", "2023-10", "2023-10", "2023-10", "2023-10", …
$ period <chr> "Weekday evening peak", "Weekday evening peak", "Weekda…
$ origin_pt_code <fct> 01012, 01013, 01019, 01029, 01039, 01059, 01109, 01112,…
$ num_trips <dbl> 8000, 7038, 3398, 9089, 12095, 2212, 276, 43513, 25769,…- mutate from dplyr package adds new variables or transforms existing ones. It’s often used in conjunction with functions like
case_whenfor conditional transformation. - case_when from dplyr package is a vectorized form of multiple
if_elsestatements, allowing for different computations or transformations based on specified conditions. - filter from dplyr package to subset rows based on specified conditions.
- group_by from dplyr package to group data by specified columns, useful for performing grouped operations like summarization.
- summarise (or
summarize) from dplyr package to calculate aggregate values for each group created bygroup_by. - rename_with from dplyr package to rename columns based on a function, such as converting names to lowercase.
- ungroup from dplyr package to remove the grouping structure from a data frame.
- glimpse from dplyr package provides a transposed summary of the data frame, offering a quick look at its contents.
3.3 Choosing the Month
In order to decide which month is better to perform LISA or whether analyzing all month separately will yield interesting result, it is a good step to check the data distribution of each month. By comparing the data distribution for each month, we can make an educated guess whether the LISA result for each month would be starkly different or just similar.
Code
# Combine odb8, odb9, and odb10 into one dataframe
combined_data <- bind_rows(
mutate(odb8, month = "odb8"),
mutate(odb9, month = "odb9"),
mutate(odb10, month = "odb10")
)
# Create a standard vertical box plot
bus_boxplot <- combined_data %>%
ggplot(aes(x = period, y = num_trips, fill = period)) + # Assigning aesthetics for x and y axes, and fill color based on period
geom_boxplot() + # Adding the box plot layer
facet_wrap(~month, scales = 'free_x') + # Faceting by month, with free scales for x axis
labs(
title = "Distribution of Trips across Peak Periods",
subtitle = "Comparison across different months",
x = "Period",
y = "Number of Trips"
) +
theme_minimal() + # Using a minimal theme for a cleaner look
theme(axis.text.x = element_blank(), axis.title.x = element_blank()) # Removing x-axis category labels and label
bus_boxplot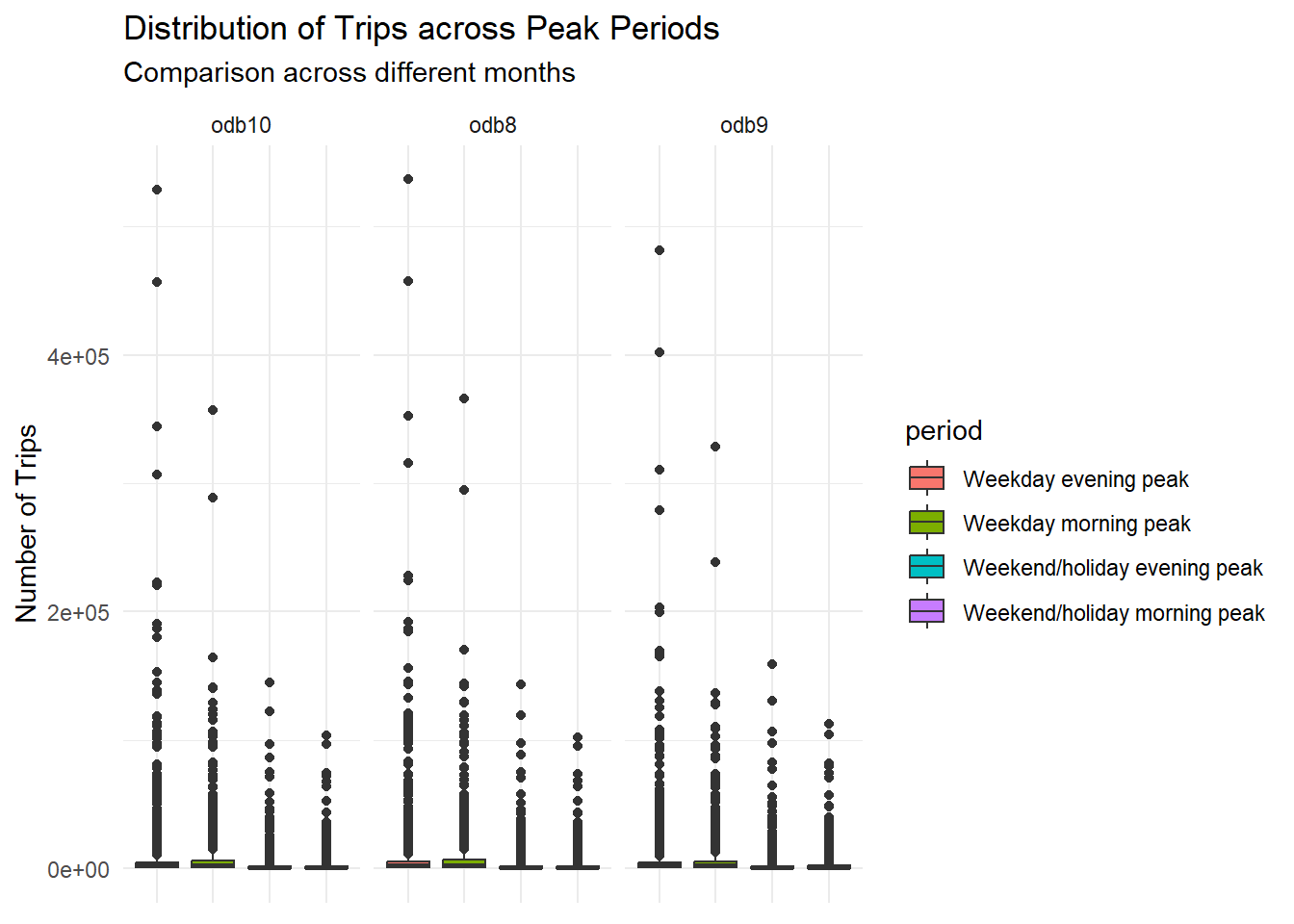
- bind_rows from dplyr package combines data frames by rows, stacking them on top of each other.
- mutate from dplyr package adds new variables or modifies existing ones in a data frame.
- ggplot from ggplot2 package creates a new ggplot graph, specifying its aesthetic mappings.
- geom_boxplot from ggplot2 package adds a boxplot layer to the ggplot.
- facet_wrap from ggplot2 package creates a facetted plot, splitting the data by one or more variables.
- labs from ggplot2 package modifies plot labels, including title and axis labels.
- theme_minimal from ggplot2 package applies a minimalistic theme to the plot.
- theme and element_blank from ggplot2 package customize aspects of the plot’s theme, such as removing axis text and titles.
The box plot to show the data distribution was not too helpful as it shows that all peak time across months has extreme outliers. Therefore, the next code chunk modify the boxplot by log-transforming the number of trips.
Code
# Create a modified vertical box plot
bus_boxplot <- combined_data %>%
ggplot(aes(x = period, y = log(num_trips), fill = period)) + # Modified aesthetics with log-transformed y-axis
geom_boxplot() + # Adding the box plot layer
facet_wrap(~month, scales = 'free_x') + # Faceting by month, with free scales for x axis
labs(
title = "Distribution of Log-Transformed Trips",
subtitle = "Comparison across different months",
y = "Log(Number of Trips)"
) +
theme_minimal() + # Using a minimal theme for a cleaner look
theme(axis.text.x = element_blank(), axis.title.x = element_blank()) # Removing x-axis category labels and label
bus_boxplot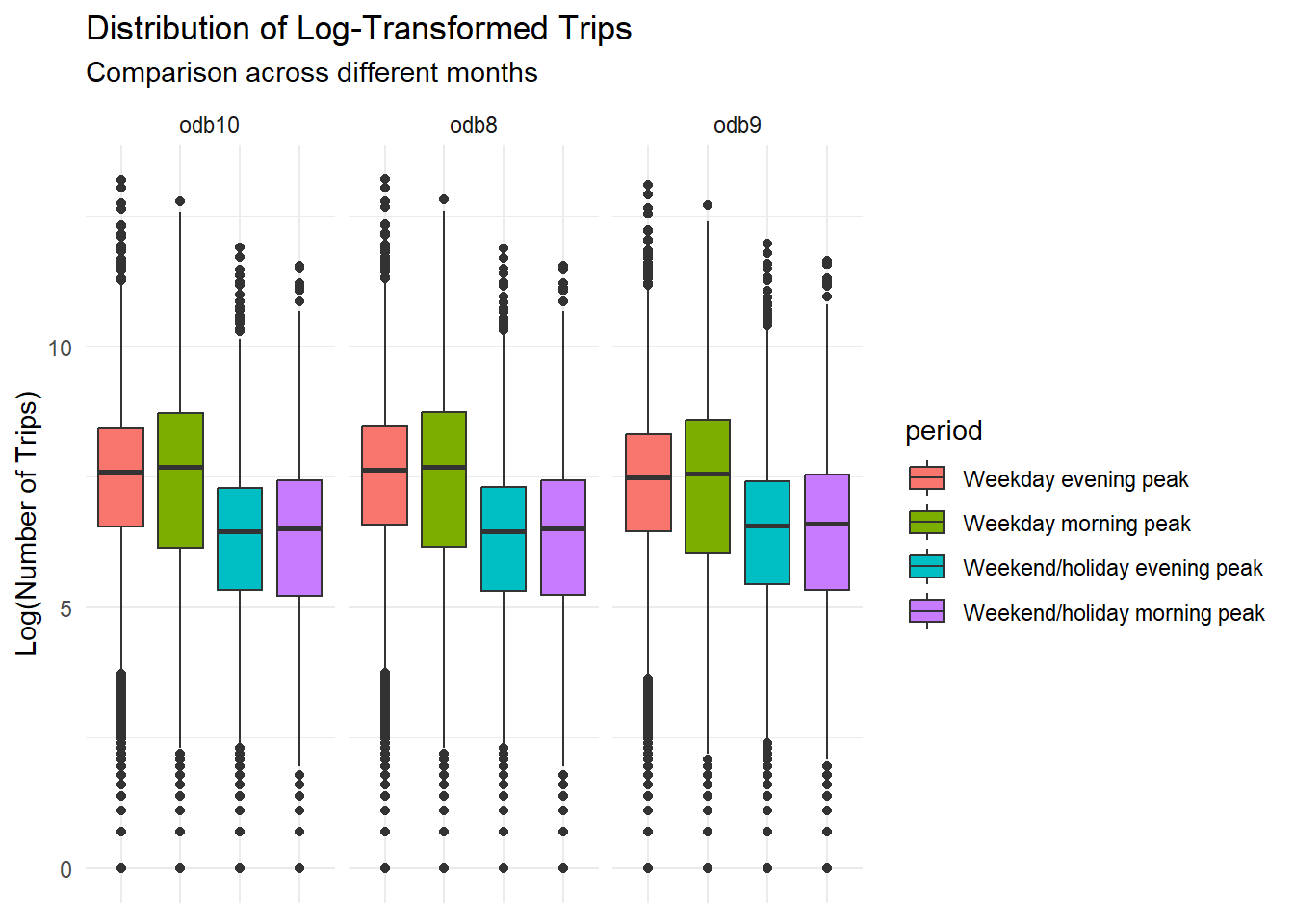
The log-transformed box plot show that the distribution of each peak periods across months is quite similar. In general, number of trips in the weekday peaks are typically higher than weekend/holiday peak. The similarity also extend to extreme outliers. For example, the green box plot (Weekday morning peak) always have a single point extreme outlier on the top of the box plot. Based on this observation, it can be inferred that performing LISA on one of month is most likely enough to discover the pattern. The month October, as the latest data available, is chosen for the next processes.
3.4 Extract Trip Numbers Into Wide Form of Peak Period Categories
Pivoting data into a wide format before merging aspatial and geospatial datasets is beneficial for streamlined analysis. It helps organize information by transforming rows into columns, making it easier to align and combine trip count data across various peak periods. This wide format simplifies subsequent data integration steps, facilitating a more efficient join between datasets based on common identifiers or keys.
Code
# Extract data from odb10 and store as a separate dataframe
odb10_wide <- odb10 %>%
# Pivot the data wider, treating each row as a bus stop code with peak period trips as columns
pivot_wider(
names_from = period,
values_from = num_trips
) %>%
select(2:6)
# check the output
DT::datatable(odb10_wide,
options = list(pageLength = 8),
rownames = FALSE)- pivot_wider from tidyr package reshapes data from a ‘long’ format to a ‘wider’ format, spreading key-value pairs across multiple columns.
- select from dplyr package is used to subset specific columns from a data frame.
- datatable from DT package creates an interactive table (data table) widget, offering functionalities like pagination. The
optionsparameter allows customization of the table, such as setting the number of rows to display per page (pageLength).
3.5 Join Aspatial and Geospatial Data
To retain the geospatial property, use left_join by using busstop as the main dataframe and bus stop code as the reference.
Code
odb10_sf <- left_join(busstop, odb10_wide, by = "origin_pt_code")
glimpse(odb10_sf)Rows: 5,144
Columns: 7
$ origin_pt_code <fct> 22069, 32071, 44331, 96081, 11561, 6619…
$ loc_desc <fct> OPP CEVA LOGISTICS, AFT TRACK 13, BLK 2…
$ `Weekday evening peak` <dbl> 67, 5, 1740, 445, 199, 349, 432, 1285, …
$ `Weekday morning peak` <dbl> 50, NA, 2075, 411, 207, 405, 60, 3059, …
$ `Weekend/holiday evening peak` <dbl> 10, NA, 589, 47, 77, 169, 82, 492, 2016…
$ `Weekend/holiday morning peak` <dbl> 8, NA, 682, 110, 70, 177, 16, 1442, 204…
$ geometry <POINT [m]> POINT (13576.31 32883.65), POINT …- left_join from dplyr package merges two data frames together based on matching values in their columns. Specifically,
left_joinkeeps all rows from the left data frame and adds matching rows from the right data frame. If there is no match, the right side will containNA. - glimpse from dplyr package provides a transposed summary of the data frame, giving a quick overview of its structure, including column types and the first few entries in each column.
3.6 Creating Hexagon Spatial Grid
odb10_sf represents a spatial point dataframe, which might not be optimal for spatial autocorrelation analysis where the definition of ‘areas’ requires the representation of spatial entities as polygons instead of individual points. To address this, the subsequent code sections transform these bus stops into a grid of hexagons.
This code utilizes the st_make_grid function to create a hexagon grid based on the specified parameters. The resulting hexagon grid is then converted into a spatial dataframe (st_sf()) to maintain its geospatial properties. The rowid_to_column function is employed to assign a unique identifier (hex_id) to each hexagon, facilitating subsequent analyses or referencing.
Output: Spatial Polygons with Hexagonal Geometry and Hex_id Identification
Code
odb10_hex <- st_make_grid(
odb10_sf,
cellsize = 500,
square = FALSE
) %>%
st_sf() %>%
rowid_to_column("hex_id")
# check the output
glimpse(odb10_hex)Rows: 5,580
Columns: 2
$ hex_id <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
$ geometry <POLYGON [m]> POLYGON ((3720.122 26626.44..., POLYGON ((3720.122 27…- st_make_grid from sf package creates a grid over a spatial object. In this code, it is used to generate a hexagonal grid over the
odb10_sfspatial data, with each cell having a size of 500 units. - st_sf from sf package converts the grid into an
sf(simple features) object, which is a standard format for handling spatial data in R. - rowid_to_column from tibble package adds a new column to a data frame that contains a unique identifier for each row.
- glimpse from dplyr package provides a transposed summary of the data frame, offering a quick look at its structure and contents.
Given that each hexagonal area may encompass multiple bus stops, the hex_id serves as the primary key for aggregation. The subsequent procedures outline how to organize attributes based on hex_id:
- Utilize the
st_join()function withjoin = st_withinto associate bus stop points with hexagon areas. - The
st_set_geometry(NULL)argument eliminates the geospatial layer, focusing on attribute aggregation. - Employ
group_by()to obtain a uniquehex_idfor each row. - Utilize
summarise()to calculate the aggregate count of bus stops and trips per peak period within each hexagon area. - Replace all
NAvalues with 0 usingreplace(is.na(.), 0).
Output: Attribute Dataframe, with Hex_id as the Primary Key
Code
odb10_stops <- st_join(
odb10_sf,
odb10_hex,
join = st_within
) %>%
st_set_geometry(NULL) %>%
group_by(hex_id) %>%
summarise(
n_busstops = n(),
busstops_code = str_c(origin_pt_code, collapse = ","),
loc_desc = str_c(loc_desc, collapse = ","),
`Weekday morning peak` = sum(`Weekday morning peak`, na.rm = TRUE),
`Weekday evening peak` = sum(`Weekday evening peak`, na.rm = TRUE),
`Weekend/holiday morning peak` = sum(`Weekend/holiday morning peak`, na.rm = TRUE),
`Weekend/holiday evening peak` = sum(`Weekend/holiday evening peak`, na.rm = TRUE)
) %>%
ungroup() %>%
mutate(across(where(is.numeric), ~ replace_na(., 0)),
across(where(is.character), ~ replace_na(., "")))
# check the output
glimpse(odb10_stops)Rows: 1,524
Columns: 8
$ hex_id <int> 34, 65, 99, 127, 129, 130, 131, 159, 16…
$ n_busstops <int> 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 2, 1, 1, …
$ busstops_code <chr> "25059", "25751", "26379", "25761", "25…
$ loc_desc <chr> "AFT TUAS STH BLVD", "BEF TUAS STH AVE …
$ `Weekday morning peak` <dbl> 103, 52, 78, 185, 1116, 53, 60, 64, 251…
$ `Weekday evening peak` <dbl> 390, 114, 291, 1905, 2899, 241, 368, 29…
$ `Weekend/holiday morning peak` <dbl> 0, 26, 52, 187, 455, 76, 45, 21, 39, 69…
$ `Weekend/holiday evening peak` <dbl> 56, 14, 100, 346, 634, 55, 49, 53, 132,…- st_join from sf package spatially joins two
sfobjects.st_withinas the join method checks if geometries of the first object are within those of the second. - st_set_geometry from sf package is used to remove or set the geometry column in an
sfobject. - group_by from dplyr package to group the data by specified columns, allowing for grouped summaries.
- summarise from dplyr package calculates summary statistics for each group.
- str_c from stringr package concatenates character vectors.
- ungroup from dplyr package removes grouping.
- mutate and across from dplyr package modify columns, applying functions across selected columns.
- replace_na from tidyr package replaces
NAvalues with specified values. - glimpse from dplyr package provides a transposed summary of the data frame.
- Use
left_jointo combine the new odb10_stops attribute dataframe with the existing odb10_hex hexagon geospatial layer, linking them by hex_id to integrate attributes into the spatial polygon dataframe. - Employ
filterto exclude hexagons without bus stops.
Output: Spatial Polygon Dataframe
Code
odb10_complete <- odb10_hex %>%
left_join(odb10_stops,
by = "hex_id"
) %>%
replace(is.na(.), 0)
odb10_final <- filter(odb10_complete,
n_busstops > 0)
# check the output
glimpse(odb10_final)Rows: 1,524
Columns: 9
$ hex_id <int> 34, 65, 99, 127, 129, 130, 131, 159, 16…
$ n_busstops <dbl> 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 2, 1, 1, …
$ busstops_code <chr> "25059", "25751", "26379", "25761", "25…
$ loc_desc <chr> "AFT TUAS STH BLVD", "BEF TUAS STH AVE …
$ `Weekday morning peak` <dbl> 103, 52, 78, 185, 1116, 53, 60, 64, 251…
$ `Weekday evening peak` <dbl> 390, 114, 291, 1905, 2899, 241, 368, 29…
$ `Weekend/holiday morning peak` <dbl> 0, 26, 52, 187, 455, 76, 45, 21, 39, 69…
$ `Weekend/holiday evening peak` <dbl> 56, 14, 100, 346, 634, 55, 49, 53, 132,…
$ geometry <POLYGON [m]> POLYGON ((3970.122 27925.48...,…4 Making Sense of the Data (GeoVisualization and Analysis)
In this section, several geovisualization will be shown to analyze the distribution and general patterns of bus stops and trips in the dataset.
4.1 Distribution of Bus Stop
Understanding the spatial distribution of bus stops in Singapore is crucial for deciphering the accessibility and connectivity of public transportation. The “Distribution of Bus Stops” map provides a visual representation of the number of bus stops across different regions.
Code
# Plot the hexagon grid based on n_busstops
tmap_mode("plot")
busstop_map = tm_shape(odb10_final)+
tm_fill(
col = "n_busstops",
palette = "Blues",
style = "cont",
title = "Number of Bus Stops",
id = "loc_desc",
showNA = FALSE,
alpha = 0.6,
popup.format = list(
grid_id = list(format = "f", digits = 0)
)
)+
tm_borders(col = "grey40", lwd = 0.7)
busstop_map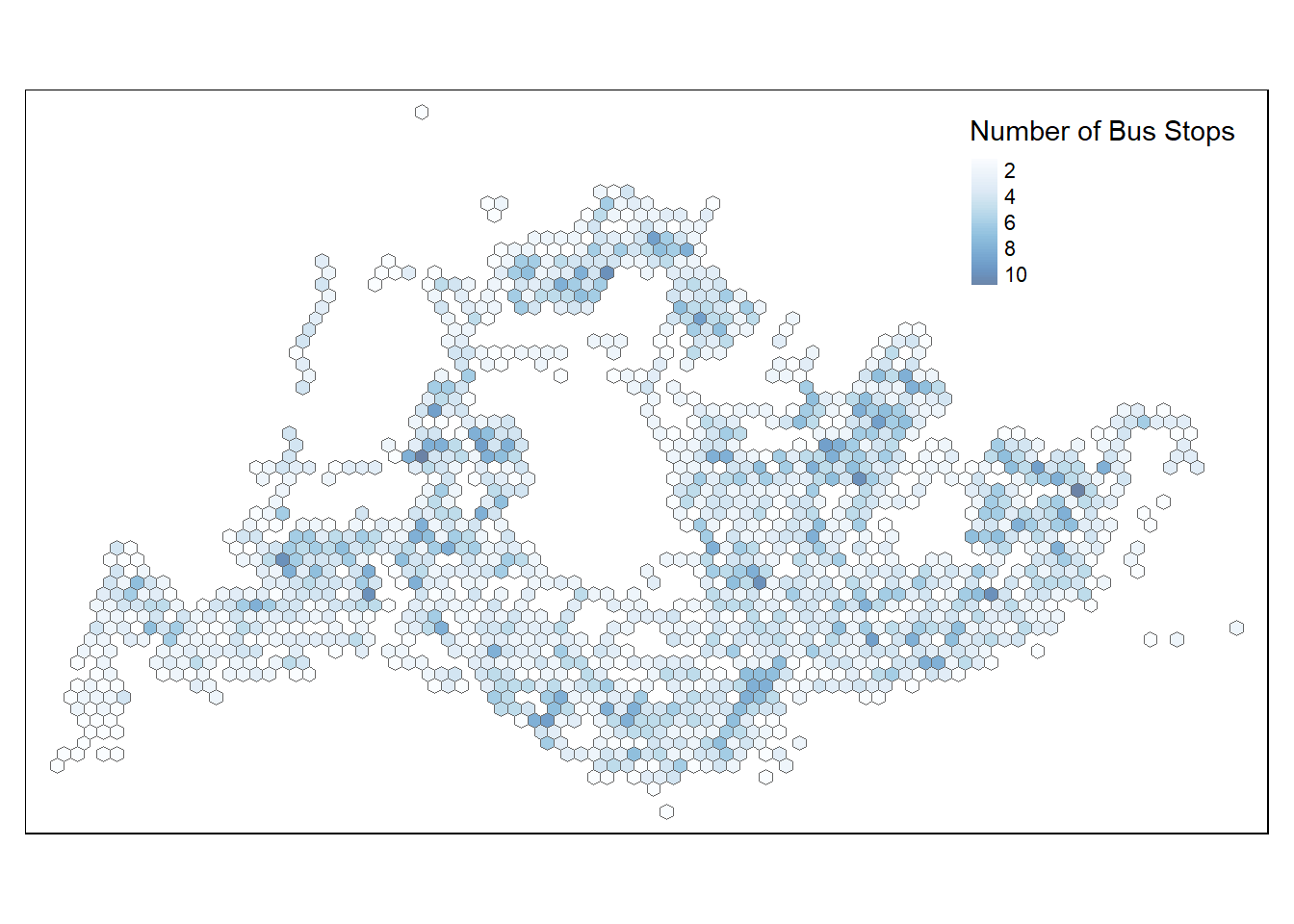
- tmap_mode from tmap package sets the mode of tmap to either plot static maps (
"plot") or create interactive maps ("view"). - tm_shape from tmap package prepares the spatial data for plotting.
- tm_fill from tmap package fills polygons (like the hexagons in the grid) with colors based on a specified variable.
- tm_borders from tmap package adds borders around the polygons.
- The
popup.formatwithintm_fillallows customization of the format of the values shown in the interactive popups.
From the map, we can infer that the central region, likely encompassing the Central Business District (CBD) and surrounding residential areas, which are known to be highly populated and active, has a higher number of bus stops. This correlates with the need for robust public transportation in densely populated areas to support the daily commute of residents and workers. Lighter shades are observed towards the periphery of the island, suggesting fewer bus stops, which could correspond to less urbanized or industrial areas, like the Western and North-Eastern regions where the population density is lower. The map reflects Singapore’s urban planning and transportation strategy, which aims to provide accessibility and connectivity, particularly in high-density regions where demand for public transit is greatest.
4.2 Distribution of Trips Across Peak Hours
find the ideal breaks for plotting the trips using summary
Code
summary(odb10_final) hex_id n_busstops busstops_code loc_desc
Min. : 34 Min. : 1.000 Length:1524 Length:1524
1st Qu.:1941 1st Qu.: 2.000 Class :character Class :character
Median :2950 Median : 3.000 Mode :character Mode :character
Mean :2814 Mean : 3.375
3rd Qu.:3735 3rd Qu.: 4.000
Max. :5558 Max. :11.000
Weekday morning peak Weekday evening peak Weekend/holiday morning peak
Min. : 0 Min. : 0 Min. : 0
1st Qu.: 919 1st Qu.: 2148 1st Qu.: 390
Median : 7611 Median : 7216 Median : 2172
Mean : 16839 Mean : 16137 Mean : 4987
3rd Qu.: 22999 3rd Qu.: 16947 3rd Qu.: 6291
Max. :386450 Max. :542529 Max. :109329
Weekend/holiday evening peak geometry
Min. : 0.0 POLYGON :1524
1st Qu.: 533.8 epsg:3414 : 0
Median : 2169.0 +proj=tmer...: 0
Mean : 4999.7
3rd Qu.: 5449.8
Max. :150399.0 The summary result confirmed that the trips data is right-skewed and contains extreme outliers. This knowledge is then used to customize the break in the comparison map.
The following code plot the comparison map. the map can be set on “plot” mode for lighter rendering, but was set on “view” mode for analysis.
Code
# Define the columns for which we want to find the global min and max
value_columns <- c("Weekday morning peak", "Weekday evening peak", "Weekend/holiday morning peak", "Weekend/holiday evening peak")
# Set tmap to interactive viewing mode for analysis and plot mode for rendering
tmap_mode("plot")
# Define a function to create each map with a customized legend
create_map <- function(value_column) {
tm_shape(odb10_final) +
tm_fill(
col = value_column,
palette = "-RdBu",
style = "fixed",
title = value_column,
id = "loc_desc",
showNA = FALSE,
alpha = 0.6,
breaks = c(0, 500, 1000, 2000, 3000, 5000, 10000, 50000, 100000, 300000, 550000)
) +
tm_borders(col = "grey40", lwd = 0.7) +
tm_layout(
legend.position = c("right", "bottom"), # Adjust legend position
legend.frame = TRUE,
legend.width = 0.15, # Adjust the width of the legend
legend.height = 0.5 # Adjust the height of the legend
)
}
# Apply the function to each value column and store the maps
map_list <- lapply(value_columns, create_map)
# Combine the maps into a 2x2 grid
combined_map <- tmap_arrange(map_list[[1]], map_list[[2]], map_list[[3]], map_list[[4]], ncol = 2, nrow = 2)
# Show the combined map
combined_map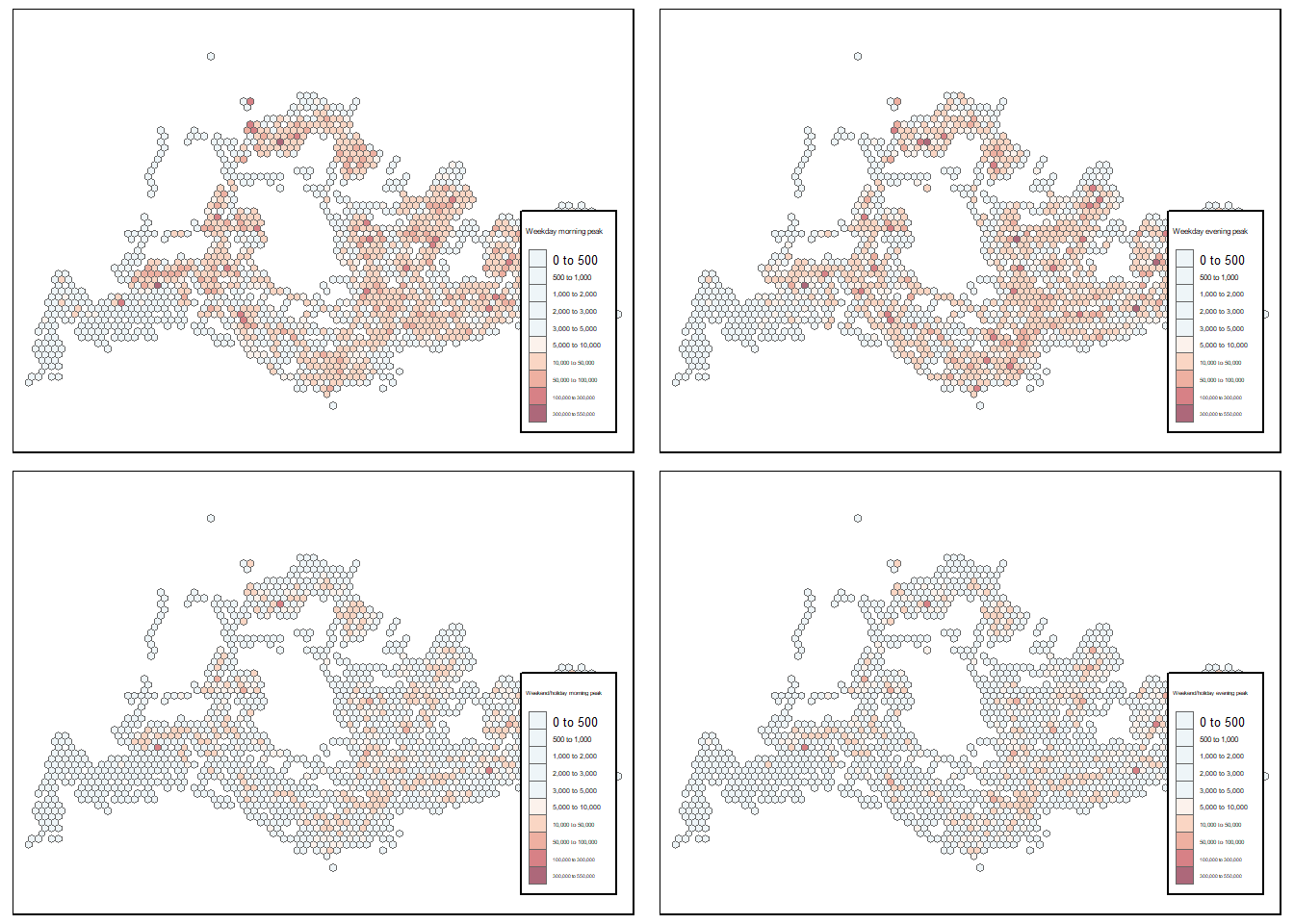
- tmap_mode from tmap package sets the mode for creating maps. Here,
"plot"mode is chosen for static map plotting. - tm_shape from tmap package prepares spatial data for plotting.
- tm_fill from tmap package fills polygons with colors based on specified variables, with options for color palette, style, and legend customization.
- tm_borders from tmap package adds borders to the polygons.
- tm_layout from tmap package adjusts the layout of the map, including legend positioning and dimensions.
- tmap_arrange from tmap package arranges multiple
tmapobjects into a grid layout. - lapply from base R applies a function over a list or vector.
Using the same classification scaling for all maps, it clearly shows that weekdays trips volume is higher in general than weekend/holiday. Nevertheless, at a glance, the crowded area are more or less the same across all days and time. This confirmed the previous finding on bus stops in which the area with most traffics are likely to encompassing the Central Business District (CBD) and surrounding residential areas, which are known to be highly populated and active the area of Singapore. At the same time, it also reflects Singapore’s urban planning and transportation strategy, in which the busiest area with potential high traffics are supported by more bus stops.
4.3 Distribution of Average Trips per Bus Stop
The next distribution will see which bus stop is the busiest on average, in terms of number of trips per bus stop. To do that, firstly the following code will generate new columns of trip per bus stop for each hexagon.
Code
# Create a new dataframe with transformed columns
odb10_final_avg <- odb10_final %>%
mutate(across(all_of(value_columns), ~ .x / n_busstops, .names = "avg_{.col}"))
# check the summary for determining break points
summary(odb10_final_avg) hex_id n_busstops busstops_code loc_desc
Min. : 34 Min. : 1.000 Length:1524 Length:1524
1st Qu.:1941 1st Qu.: 2.000 Class :character Class :character
Median :2950 Median : 3.000 Mode :character Mode :character
Mean :2814 Mean : 3.375
3rd Qu.:3735 3rd Qu.: 4.000
Max. :5558 Max. :11.000
Weekday morning peak Weekday evening peak Weekend/holiday morning peak
Min. : 0 Min. : 0 Min. : 0
1st Qu.: 919 1st Qu.: 2148 1st Qu.: 390
Median : 7611 Median : 7216 Median : 2172
Mean : 16839 Mean : 16137 Mean : 4987
3rd Qu.: 22999 3rd Qu.: 16947 3rd Qu.: 6291
Max. :386450 Max. :542529 Max. :109329
Weekend/holiday evening peak geometry avg_Weekday morning peak
Min. : 0.0 POLYGON :1524 Min. : 0.0
1st Qu.: 533.8 epsg:3414 : 0 1st Qu.: 395.2
Median : 2169.0 +proj=tmer...: 0 Median : 2609.4
Mean : 4999.7 Mean : 4520.1
3rd Qu.: 5449.8 3rd Qu.: 6138.6
Max. :150399.0 Max. :119816.0
avg_Weekday evening peak avg_Weekend/holiday morning peak
Min. : 0.0 Min. : 0.0
1st Qu.: 954.3 1st Qu.: 166.2
Median : 2285.9 Median : 775.0
Mean : 4423.1 Mean : 1351.3
3rd Qu.: 4575.0 3rd Qu.: 1659.1
Max. :136001.0 Max. :43420.0
avg_Weekend/holiday evening peak
Min. : 0.0
1st Qu.: 224.9
Median : 713.6
Mean : 1381.3
3rd Qu.: 1473.2
Max. :39425.0 - mutate from dplyr package is used to add new columns to a data frame or modify existing ones.
- across from dplyr package applies a function to a selection of columns, in this case, transforming specified columns by dividing each by
n_busstops. - all_of from dplyr package is used within
acrossfor selecting columns based on a character vector of column names. - summary from base R provides a summary of the object’s contents, typically giving minimum, maximum, mean, and other useful statistics.
The following code plot the comparison map. the map is set on “plot” mode for rendering, but was set on “view” mode for analysis.
Code
# Define the columns for which we want to find the global min and max
value_columns <- c("avg_Weekday morning peak", "avg_Weekday evening peak", "avg_Weekend/holiday morning peak", "avg_Weekend/holiday evening peak")
# Set tmap to interactive viewing mode
tmap_mode("plot")
# Define a function to create each map with a customized legend
create_map <- function(value_column) {
tm_shape(odb10_final_avg) +
tm_fill(
col = value_column,
palette = "-RdBu",
style = "fixed",
title = value_column,
id = "loc_desc",
showNA = FALSE,
alpha = 0.6,
breaks = c(0, 100, 200, 300, 400, 500, 750, 1000, 1500, 5000, 10000, 50000, 140000)
) +
tm_borders(col = "grey40", lwd = 0.7) +
tm_layout(
legend.position = c("right", "bottom"), # Adjust legend position
legend.frame = TRUE,
legend.width = 0.15, # Adjust the width of the legend
legend.height = 0.5 # Adjust the height of the legend
)
}
# Apply the function to each value column and store the maps
map_list <- lapply(value_columns, create_map)
# Combine the maps into a 2x2 grid
combined_map <- tmap_arrange(map_list[[1]], map_list[[2]], map_list[[3]], map_list[[4]], ncol = 2, nrow = 2)
# Show the combined map
combined_map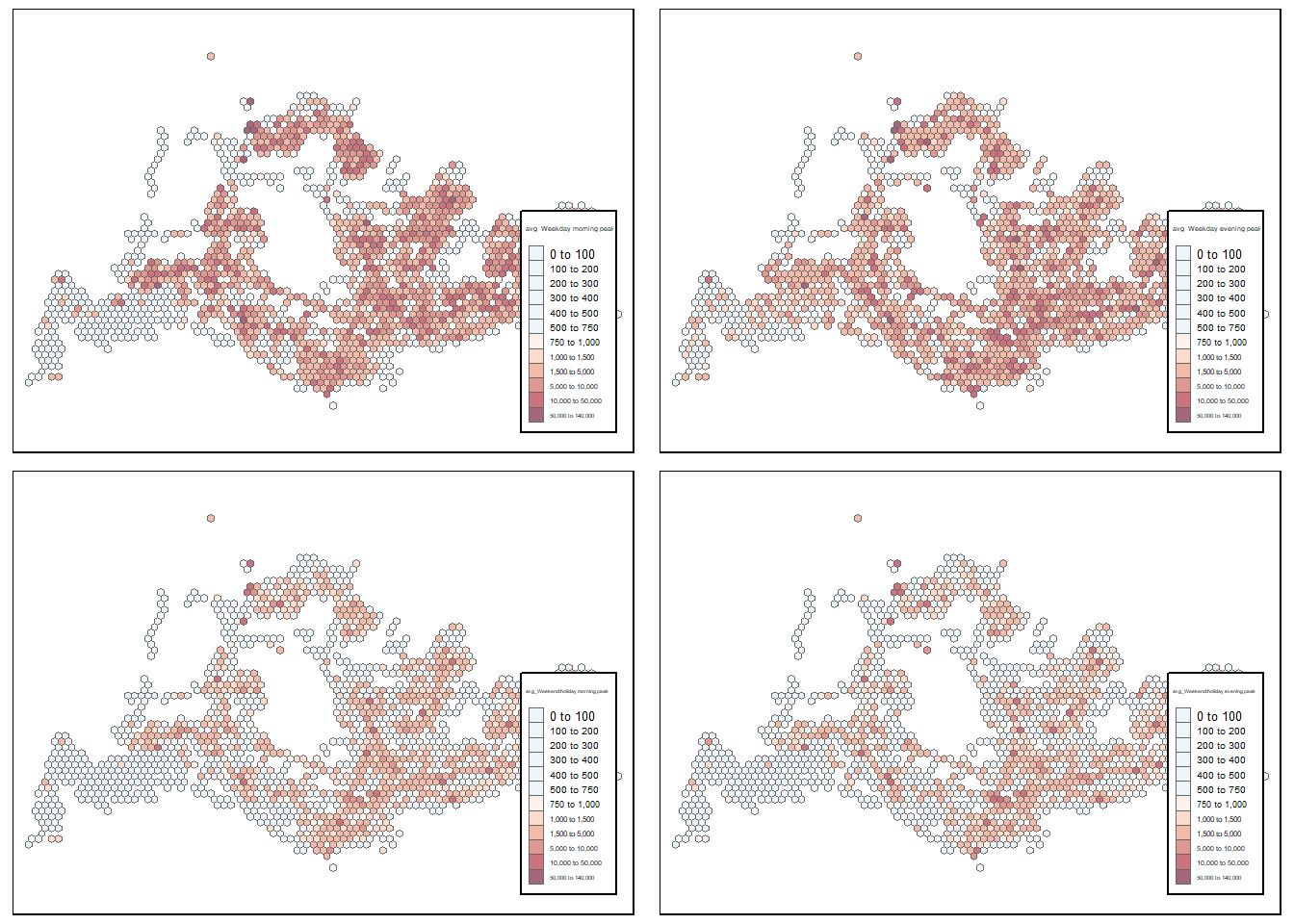
- tmap_mode from tmap package sets the mode for creating maps.
"plot"mode is used for static map plotting. - tm_shape from tmap package prepares spatial data for plotting.
- tm_fill from tmap package fills polygons with colors based on specified variables, allowing for customized legends and color palettes.
- tm_borders from tmap package adds borders to the polygons.
- tm_layout from tmap package adjusts the layout of the map, including legend position and dimensions.
- lapply from base R applies a function over a list or vector.
- tmap_arrange from tmap package arranges multiple
tmapobjects into a grid layout.
at a glance, using the average trips per bus stop shows slightly different insight. Comparatively to the total trips, average number of trips shows that the area around Jurong, Woodlands, and bus stops in Johor (part of Malaysia) is actually busier than what total trips suggest. In the context of transport policy, this might be the first lead to expand the number of bus stops in the particular area to cater for more commuters.
5 Local Indicators of Spatial Association analysis
In this segment, we’ll utilize Local Indicators of Spatial Association (LISA) metrics to investigate whether clusters or anomalies exist in the overall number of trips generated within the hexagon layer. More precisely, we’ll employ Moran’s I statistic to identify spatial patterns, including the presence of clusters or dispersion in the total trip counts.
5.1 Creating a Spatial Matrix Based on Distance
Before we delve into the intricacies of global and local spatial autocorrelation statistics, a crucial preliminary step involves the creation of a spatial weights matrix tailored to our study area. This matrix essentially delineates the relationships between hexagonal spatial units based on their respective distances. In establishing this matrix, it’s imperative to bear in mind a few considerations.
Firstly, it is essential to ensure that each feature has at least one neighbor, and conversely, no feature is designated as a neighbor to all other features. This ensures a meaningful and diverse representation of spatial relationships.
Furthermore, for datasets exhibiting skewed distribution, a recommended guideline is to assign each feature a minimum of eight neighbors, a criterion we’ve slightly exceeded by opting for 12 neighbors in this context. This ensures a more robust and comprehensive understanding of spatial connectivity within the data.
Given the peculiarities of our study area, characterized by regions with a sparse distribution of bus stops, particularly in zones lacking significant residential or business presence, the preference leans towards employing distance-based methods over contiguity methods. This strategic choice aligns with the spatial reality of the data, allowing for a more nuanced exploration of spatial relationships while considering the unique characteristics of the geographical context.
We opt for the Adaptive Distance-Based (Fixed Number of Neighbors) approach instead of the Fixed-Distance Threshold method, a decision prompted by the right-skewed distribution inherent in our dataset. In this chosen method, each hexagon is assured of having a minimum of n neighbors, a critical prerequisite for subsequent statistical significance testing.
To implement this, we set each hexagon to be associated with precisely 12 neighbors, a configuration achieved through the application of provided R code. The process involves utilizing the st_knn function to acquire a comprehensive list of neighbors for each hexagon and subsequently employing st_weights to generate spatial weights that are row-standardized. This meticulous procedure ensures a standardized and well-defined spatial relationship framework, laying the groundwork for robust statistical analyses.
Code
wm_all <- odb10_final %>%
mutate(
nb = st_knn(geometry, k = 12),
wt = st_weights(nb, style = 'W'),
.before = 1
)
# check the output
kable(head(wm_all))| nb | wt | hex_id | n_busstops | busstops_code | loc_desc | Weekday morning peak | Weekday evening peak | Weekend/holiday morning peak | Weekend/holiday evening peak | geometry |
|---|---|---|---|---|---|---|---|---|---|---|
| 2, 4, 5, 8, 9, 12, 13, 16, 22, 23, 38, 39 | 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333 | 34 | 1 | 25059 | AFT TUAS STH BLVD | 103 | 390 | 0 | 56 | POLYGON ((3970.122 27925.48… |
| 1, 3, 4, 5, 8, 9, 12, 13, 16, 22, 23, 38 | 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333 | 65 | 1 | 25751 | BEF TUAS STH AVE 14 | 52 | 114 | 26 | 14 | POLYGON ((4220.122 28358.49… |
| 5, 6, 7, 9, 10, 13, 14, 16, 17, 18, 24, 25 | 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333 | 99 | 1 | 26379 | YONG NAM | 78 | 291 | 52 | 100 | POLYGON ((4470.122 30523.55… |
| 1, 2, 5, 8, 9, 12, 13, 16, 22, 23, 38, 39 | 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333 | 127 | 1 | 25761 | OPP REC S’PORE | 185 | 1905 | 187 | 346 | POLYGON ((4720.122 28358.49… |
| 3, 6, 9, 10, 12, 13, 14, 16, 17, 24, 30, 31 | 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333 | 129 | 2 | 25719,26389 | THE INDEX,BEF TUAS STH AVE 5 | 1116 | 2899 | 455 | 634 | POLYGON ((4720.122 30090.54… |
| 3, 5, 7, 9, 10, 11, 13, 14, 17, 18, 24, 25 | 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333 | 130 | 1 | 26369 | SEE HUP SENG | 53 | 241 | 76 | 55 | POLYGON ((4720.122 30956.57… |
- mutate from dplyr package is used to add new columns to a data frame or modify existing ones.
- st_knn from sfdep package computes k-nearest neighbors for spatial data. Here, it is used to find the nearest 12 neighbors for each geometry in
odb10_final. - st_weights from sfdep computes spatial weights. The
style = 'W'argument specifies the type of weights to be calculated. - The
.before = 1argument inmutatespecifies that the new columns should be added at the beginning of the data frame. - kable from the knitr package creates simple tables from a data frame for markdown format output.
5.2 Examining Global Spatial Association Globally with Global Moran’s I
Assessing global spatial correlation involves scrutinizing the comprehensive spatial arrangement of a specific variable, such as the aggregated count of trips throughout the entire study region. This analysis furnishes a solitary metric that encapsulates how closely akin values aggregate or scatter across the geographic expanse.
Calculate the Global Moran’s I statistic for peak time trip counts at the hexagonal level, employing simulated data to sidestep assumptions of normal distribution and randomness. The simulation count is established at 99+1, totaling 100 simulations, ensuring a robust evaluation of spatial relationships without reliance on normality or random distribution assumptions.
Code
# Set the seed to ensure reproducibility
set.seed(1234)
# define the value_columns
value_columns <- c("Weekday morning peak", "Weekday evening peak", "Weekend/holiday morning peak", "Weekend/holiday evening peak")
# Create a function to perform global Moran's I test
perform_global_moran <- function(data, value_column, k) {
# Compute spatial weights
nb <- st_knn(data$geometry, k = k)
wt <- st_weights(nb, style = 'W')
# Perform global Moran's I test
moran_result <- global_moran_perm(data[[value_column]], nb, wt, nsim = 99)
# Include the value_column in the result
result <- list(
value_column = value_column,
moran_result = moran_result
)
return(result)
}
# Apply the function for each time interval
results <- lapply(value_columns, function(vc) perform_global_moran(wm_all, vc, k = 12))
# Print the results
print(results)[[1]]
[[1]]$value_column
[1] "Weekday morning peak"
[[1]]$moran_result
Monte-Carlo simulation of Moran I
data: x
weights: listw
number of simulations + 1: 100
statistic = 0.18577, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sided
[[2]]
[[2]]$value_column
[1] "Weekday evening peak"
[[2]]$moran_result
Monte-Carlo simulation of Moran I
data: x
weights: listw
number of simulations + 1: 100
statistic = 0.044513, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sided
[[3]]
[[3]]$value_column
[1] "Weekend/holiday morning peak"
[[3]]$moran_result
Monte-Carlo simulation of Moran I
data: x
weights: listw
number of simulations + 1: 100
statistic = 0.13802, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sided
[[4]]
[[4]]$value_column
[1] "Weekend/holiday evening peak"
[[4]]$moran_result
Monte-Carlo simulation of Moran I
data: x
weights: listw
number of simulations + 1: 100
statistic = 0.084176, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sided- set.seed from base R package is used to set the seed of R’s random number generator, ensuring reproducibility of results.
- st_knn from sfdep package computes k-nearest neighbors for spatial data, used here to create spatial weights.
- st_weights from sfdep package calculates spatial weights. The
style = 'W'argument specifies the type of weights. - global_moran_perm from fpdep package performs a permutation test for global Moran’s I, a measure of spatial autocorrelation.
- lapply from base R applies a function over a list or vector.
For all four time intervals, since the p-value for global Moran’s I is smaller than 0.05, we can reject the null hypothesis that the spatial patterns are random. Moreover, as the Moran’s I statistics are greater than 0, we can infer that the spatial distribution exhibits signs of clustering for all four time intervals, consistent with the choropleth maps plotted earlier.
5.3 Assessing Local Autocorrelation Spatial Association
Delving into local spatial relationships offers a nuanced exploration of spatial configurations at a granular level, pinpointing particular zones with pronounced or diminished spatial connections. The Local Moran’s I method classifies areas into distinct categories such as high-high, low-low, high-low, or low-high, delineating patterns of clustering or outlier behavior within specific regions.
To analyze passenger trip patterns originating at the hex level, we employ the Local Indicators of Spatial Association (LISA) through the local_moran function sourced from the sfdep package. This function automatically computes neighbor lists and weights, leveraging simulated data to enhance accuracy. The outcomes are then deconstructed for in-depth analysis and presented in an interactive datatable format, allowing for a comprehensive examination of the intricacies within the spatial relationships of passenger trips.
Code
# Create a function to perform local Moran's I analysis
get_lisa <- function(wm, value_column, k) {
# Compute spatial weights
nb <- st_knn(wm$geometry, k = k)
wt <- st_weights(nb, style = 'W')
# Perform local Moran's I analysis and create a new data frame
result <- wm %>%
mutate(
local_moran = local_moran(.data[[value_column]], nb, wt, nsim = 99),
.before = 1
) %>%
unnest(local_moran)
return(result)
}
# Initialize a list to store results for each value_column
lisa_results <- list()
# Apply the function for each time interval and store results in the list
for (vc in value_columns) {
lisa_results[[vc]] <- get_lisa(wm_all, vc, k = 12)
# Remove columns that don't belong to the specific time interval
unwanted_columns <- setdiff(value_columns, vc)
lisa_results[[vc]] <- lisa_results[[vc]][, !(names(lisa_results[[vc]]) %in% unwanted_columns)]
}
# show sample output in an interactive table
datatable(lisa_results[["Weekday morning peak"]],
class = 'cell-border stripe',
options = list(pageLength = 5))- st_knn from sfdep package computes k-nearest neighbors for spatial data, used here for spatial weights calculation.
- st_weights from sfdep package creates spatial weights with the specified style (
'W'). - local_moran from sfdep package performs local Moran’s I analysis, a measure of local spatial autocorrelation.
- mutate and unnest from dplyr and tidyr respectively, are used to modify and expand nested data within a data frame.
- datatable from DT package creates an interactive table widget.
- The
forloop in base R iteratively applies theget_lisafunction to each value column.
5.4 Significant Local Moran’s I Results at α 5%
Leverage the fundamental functionalities of the tmap package to create choropleth maps illustrating the Local Moran’s I field and p-value field across all four time intervals. Only noteworthy values of Local Moran’s I at a significance level of α 5% are visualized. The provided code retrieves the pertinent Local Moran’s I values for the explicit purpose of generating maps.
Code
get_sig_lmi_map <- function(lisa_table, title) {
sig_lisa_table <- lisa_table %>%
filter(p_ii_sim < 0.05)
result <- tm_shape(lisa_table) +
tm_polygons() +
tm_borders(alpha = 0.5) +
tm_shape(sig_lisa_table) +
tm_fill("ii") +
tm_borders(alpha = 0.4) +
tm_layout(
main.title = title,
main.title.size = 1.3
)
return(result)
}
sig_lmi_1 <- get_sig_lmi_map(lisa_results[["Weekday morning peak"]], "Weekday Morning" )
sig_lmi_2 <- get_sig_lmi_map(lisa_results[["Weekday evening peak"]], "Weekday Afternoon" )
sig_lmi_3 <- get_sig_lmi_map(lisa_results[["Weekend/holiday morning peak"]], "Weekend Morning" )
sig_lmi_4 <- get_sig_lmi_map(lisa_results[["Weekend/holiday morning peak"]], "Weekend Afternoon" )
tmap_mode('view')
tmap_arrange(
sig_lmi_1,
sig_lmi_2,
sig_lmi_3,
sig_lmi_4,
asp = 2,
nrow = 2,
ncol = 2
)- filter from dplyr package to subset rows based on a condition, here filtering for statistically significant local Moran’s I results.
- tm_shape, tm_polygons, tm_borders, tm_fill, and tm_layout from tmap package are used to create and customize thematic maps.
- tmap_mode sets the tmap mode, here
'plot'is for static maps. - tmap_arrange arranges multiple
tmapobjects in a grid layout.
The choropleth maps displaying Local Moran’s I reveal that darker orange and darker green areas signify outlier regions. To classify it into low-high or high-low cluster, further analysis is required using LISA. Similarly, the light green indicates either high-high or low-low regions. Notably, the the area around Tuas and Jurong is most likely a low-low area based on the previous geovisualization.
5.5 LISA Map at α 5%
For a more in-depth analysis, the subsequent code retrieves the meaningful Local Indicators of Spatial Association (LISA) for the specific purpose of creating maps.
Code
get_sig_lisa_map <- function(lisatable, title) {
sig_lisatable <- lisatable %>%
filter(p_ii_sim < 0.05)
result <- tm_shape(lisatable) +
tm_polygons(alpha = 0.5) +
tm_borders(alpha = 0.5) +
tm_shape(sig_lisatable) +
tm_fill("median",
id = "loc_desc",
palette = c("blue", "lightcoral", "lightblue", "red"),
alpha= 0.7,
title = "Cluster") +
tm_borders(alpha = 0.4) +
tm_layout(main.title = title,
main.title.size = 1.5,
legend.position = c("left", "top"))
return(result)
}
sig_lisa_1 <- get_sig_lisa_map(lisa_results[["Weekday morning peak"]],"LISA categories generated on Weekday Morning at 95% CL" )
sig_lisa_2 <- get_sig_lisa_map(lisa_results[["Weekday evening peak"]], "LISA categories generated on Weekday Afternoon at 95% CL" )
sig_lisa_3 <- get_sig_lisa_map(lisa_results[["Weekend/holiday morning peak"]], "LISA categories generated on Weekend Morning at 95% CL" )
sig_lisa_4 <- get_sig_lisa_map(lisa_results[["Weekend/holiday morning peak"]], "LISA categories generated on Weekend Afternoon at 95% CL" )In the ensuing panel, you’ll find a display featuring the noteworthy Local Indicators of Spatial Association (LISA) map corresponding to each peak time.
Code
tmap_mode('plot')
sig_lisa_1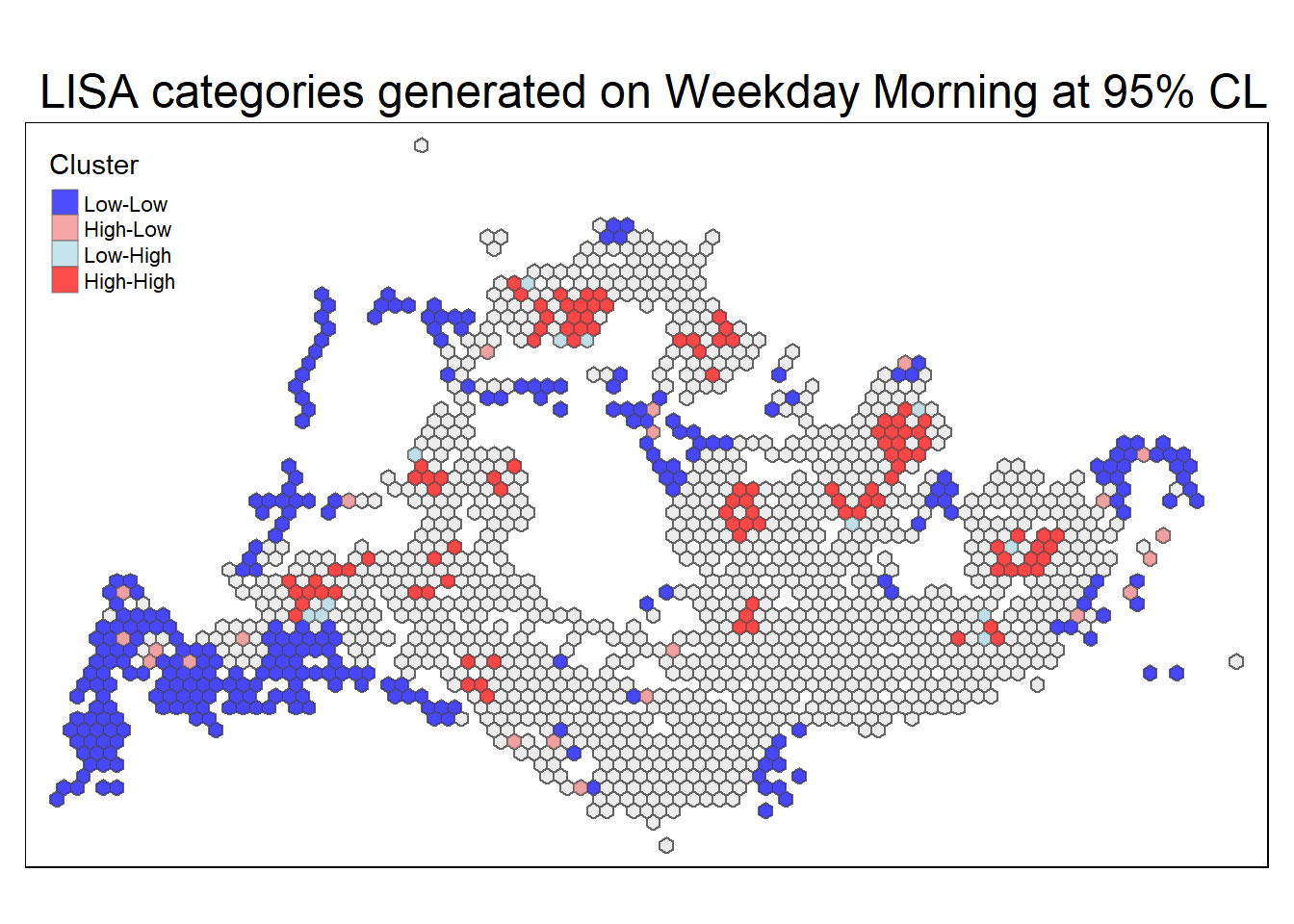
Code
tmap_mode('plot')
sig_lisa_2
Code
tmap_mode('plot')
sig_lisa_3
Code
tmap_mode('plot')
sig_lisa_1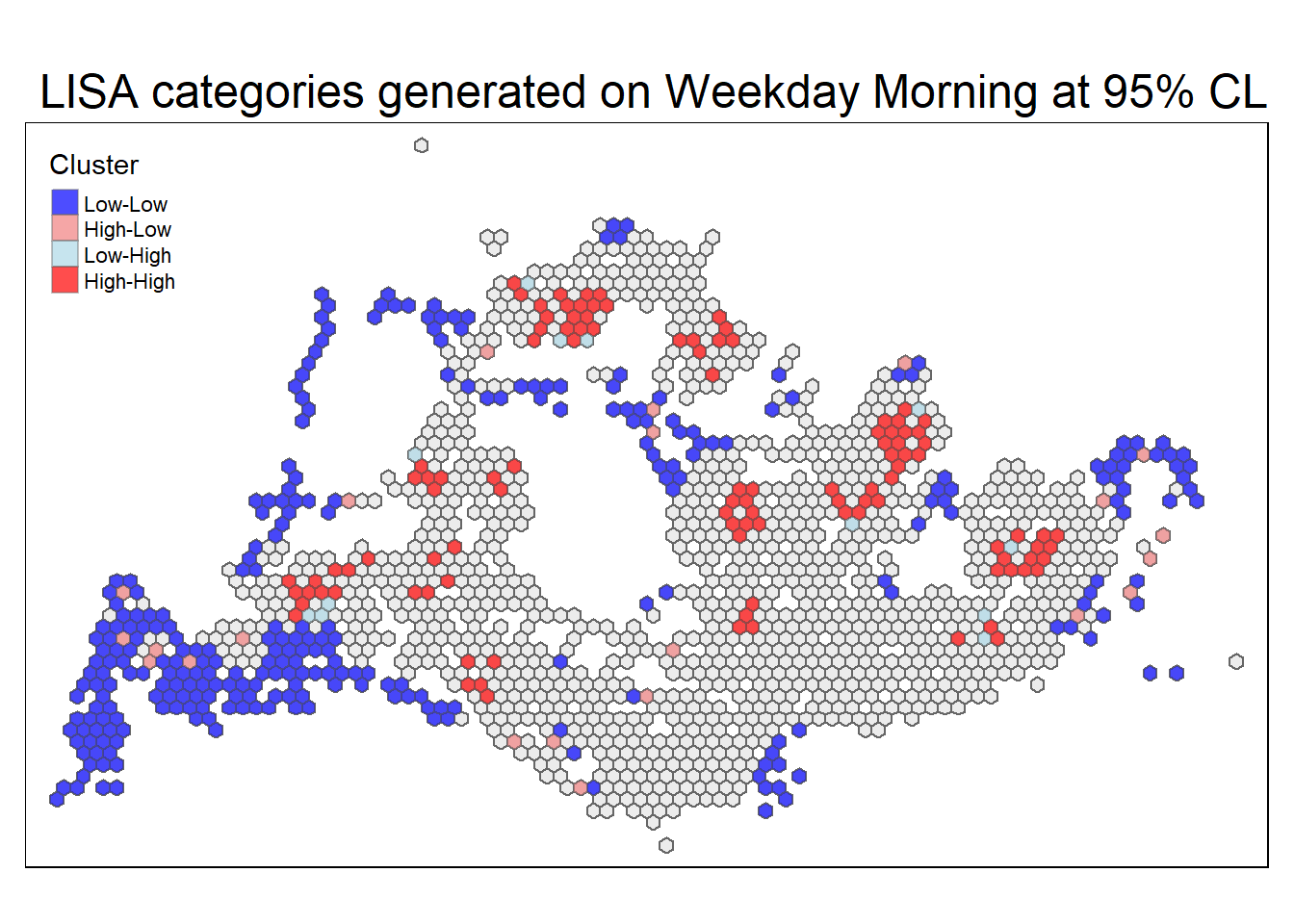
The preceding choropleth maps illustrate notable groupings and exceptional instances regarding passenger trips originating from each hexagon, applying a significance level of α 5%.
Cluster Interpretation:
Blue regions (Low-Low Clusters): These areas signify locations where the number of total trips at bus stops is relatively low and is surrounded by other locations with similarly low trip counts. This indicates spatial clustering of lower activity.Light Blue regions (Low-High outliers): In these regions, bus stops experience a lower number of total trips compared to their neighbors, suggesting an outlier pattern where specific locations have lower activity amidst areas with higher trip counts.
Light Coral regions (High-Low outliers): High-Low regions denote areas where bus stops have a higher number of total trips compared to their neighbors, standing out as outliers with higher activity within regions of lower overall trip counts.
Red regions (High-High clusters): These regions represent clusters of higher activity, where bus stops experience a higher number of total trips and are surrounded by other locations with similarly high trip counts. This implies spatial clustering of higher activity zones.
5.6 Findings and Future Improvements
The geographical arrangement unveils elevated concentrations of overall bus trips in the residential sectors situated in the East, North, and West, juxtaposed with diminished concentrations in the Southern sector of Singapore. Prominent clusters of heightened activity align with significant transportation hubs like Ang Mo Kio, Bedok, Clementi, Hougang, Toa Payoh, Woodlands, and more.
Specific hexagonal zones, notably in the vicinity of Bukit Timah and Woodlands Checkpoint, display unique trends on weekends. These areas fluctuate between instances of high-low outliers and elevated clusters, indicating dynamic shifts in bus trip patterns across varying days of the week.
High Clusters: Within the North, East, and West regions, particularly in residential zones, there is a discernible prevalence of elevated concentrations of bus trips. These areas are indicative of heightened commuting activities and increased local engagements, reflecting a probable dependence on public transportation for daily travel.
Low Clusters: Conversely, the western sectors of Singapore, predominantly consisting of industrial areas, demonstrate diminished concentrations of bus trips. This pattern hints at a lower reliance on public transportation within these industrial zones, potentially influenced by factors such as lower population density or the prevalence of alternative modes of transport. The observed lower bus trip concentrations in these regions align with a distinctive transportation landscape characterized by different travel patterns and demands.
Clusters of Low Passenger Trips: Examining the Western and Southern perimeters of Singapore, we discern notable concentrations of low passenger trips. Specifically, areas along these borders exhibit a distinct pattern of reduced public transportation usage. This phenomenon suggests a potential lower demand for bus services in these regions, indicating varying transportation preferences or alternative modes of commuting among residents.
Noteworthy Outliers and Unique Transportation Needs: Within this context, noteworthy outliers such as Jurong Port, Pioneer Sector, and Tuas stand out, marking key gateways that play a crucial role in accommodating nearby migrant workers and tourists. These specific regions may harbor unique transportation requirements, contributing significantly to the distinctive spatial patterns observed. The presence of outliers indicates a deviation from the general trend, emphasizing the importance of understanding the specific dynamics influencing transportation demand in these particular locales.
The spatial distribution of bus trips may be influenced by the availability and efficiency of alternative modes of transportation, such as the MRT (Mass Rapid Transit) system or private vehicles. Areas with robust alternative public transportation networks might exhibit different bus trip patterns compared to regions heavily reliant on private vehicles. Analyzing the interplay between different modes of transport can offer insights into the dynamics of bus trip concentrations and outliers.
Exploring the correlation between bus trip patterns and population density can unveil insights into how transportation needs align with residential density. High-density residential areas may show increased reliance on public transportation, leading to concentrated bus trip clusters. On the other hand, lower-density regions might exhibit more scattered trip patterns.
Investigating the correlation between bus trip concentrations and major economic activities or employment hubs can shed light on commuter patterns. Areas with prominent business districts or industrial zones may experience higher bus trip concentrations during peak commuting hours, contributing to spatial clusters.
Analyzing demographic factors such as age groups, income levels, and cultural preferences may provide nuanced insights into bus trip patterns. Different demographic segments may exhibit varying transportation behaviors, influencing the distribution of bus trips across different regions.
Examining the influence of urban planning and infrastructure development on bus trip patterns can highlight the impact of transportation policies and initiatives. Regions with well-planned transportation infrastructure may demonstrate more organized and efficient bus trip distributions.
Considering the impact of seasons and major events on bus trip patterns can uncover dynamic changes in spatial distributions. Certain regions may experience fluctuations in bus trip concentrations during holidays, festivals, or major events, reflecting shifts in travel behavior.
Assessing the role of technological advancements and ride-sharing trends on bus trip patterns can provide insights into the evolving landscape of transportation preferences. The integration of technology-driven solutions may influence how people choose and utilize bus services.
6 References
Andrey Sekste and Eduard Kazakov. “H3 hexagonal grid: Why we use it for data analysis and visualization”.
Anselin, L. (1995). “Local indicators of spatial association – LISA”. Geographical Analysis, 27(4): 93-115.
Sarah Gates (2017). “Emerging Hot Spot Analysis: Finding Patterns over Space and Time”
Sid Dhuri (2020). “Spatial Data Analysis With Hexagonal Grids”
Tin Seong Kam. “2 Choropleth Mapping with R” From R for Geospatial Data Science and Analytics
Tin Seong Kam. “9 Global Measures of Spatial Autocorrelation” From R for Geospatial Data Science and Analytics
Tin Seong Kam. “10 Local Measures of Spatial Autocorrelation” From R for Geospatial Data Science and Analytics
Land Transport Authority. Land Transport Data Mall
Wong, Kenneth. Create spatial square/hexagon grids and count points inside in R with sf from Urban Data Pallete