Hands-on Exercise 1: Geospatial Data Wrangling with R

Author

Muhamad Ameer Noor

Published

November 17, 2023

Modified

December 14, 2023

1 Overview

This hands-on exercise is about importing and wrangling geospatial data using appropriate R packages.

2 Getting Started

The code chunk below install and load sf and tidyverse packages into R environment.

pacman::p_load(sf, tidyverse, tmap)

3 Importing Geospatial Data

The data import process uses a tool called st_read. It is a function to read different types of maps, in the format/extension such as .shp, .dbf, .prj, and .shx. The function use the following parameters:

Location Instruction (dsn Parameter): This part is specifying where to find the map files. In our case, the maps are in a folder called “../data/geospatial.”
Layer Instruction (layer Parameter): This part is specifying focus on a specific aspect of the maps. Think of the maps as a big book, and a layer is like a section that talks about a particular topic. In our example, we’re interested in a section named “MP14_SUBZONE_WEB_PL,” which contains information about areas called subzones.

mpsz <- st_read(dsn = "../data/geospatial", layer = "MP14_SUBZONE_WEB_PL")

Reading layer `MP14_SUBZONE_WEB_PL' from data source 
  `C:\ameernoor\ISSS624\data\geospatial' using driver `ESRI Shapefile'
Simple feature collection with 323 features and 15 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
Projected CRS: SVY21

Shapefiles are a common geospatial vector data format used to represent geographic features such as points, lines, and polygons. In this case, MP14_SUBZONE_WEB_PL is a layer within the shapefile containing polygon features, which could represent, for example, subzones in a geographic region. The Master Plan 2014 Subzone Boundary (Web) data is a forward looking guiding plan for Singapore’s development in the medium term over the next 10 to 15 years Development Master Plan 2014. Subzones are divisions within a planning area which are usually centred around a focal point such as neighbourhood centre or activity node. There can be more than 10 subzones within a Planning Area. The data is sourced from Singapore Government

cyclingpath <- st_read(dsn = "../data/geospatial", layer = "CyclingPathGazette")

Reading layer `CyclingPathGazette' from data source 
  `C:\ameernoor\ISSS624\data\geospatial' using driver `ESRI Shapefile'
Simple feature collection with 2558 features and 2 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: 11854.32 ymin: 28347.98 xmax: 42626.09 ymax: 48948.15
Projected CRS: SVY21

This code imports polyline feature data from a shapefile. Polylines are sequences of connected straight lines and are commonly used to represent linear features such as roads, rivers, or cycling paths. In this case, the data are line representations of an intra-town path around Singapore designated for cyclists, excluding park connectors. The data is sourced from Land Transport Authority

preschool <- st_read(dsn = "../data/geospatial/PreSchoolsLocation.kml")

Reading layer `PRESCHOOLS_LOCATION' from data source 
  `C:\ameernoor\ISSS624\data\geospatial\PreSchoolsLocation.kml' 
  using driver `KML'
Simple feature collection with 2290 features and 2 fields
Geometry type: POINT
Dimension:     XYZ
Bounding box:  xmin: 103.6878 ymin: 1.247759 xmax: 103.9897 ymax: 1.462134
z_range:       zmin: 0 zmax: 0
Geodetic CRS:  WGS 84

This code import GIS (Geographic Information System) in KML format. KML (Keyhole Markup Language) is an XML-based format often used for expressing geographic annotation and visualization within Internet-based, two-dimensional maps and three-dimensional Earth browsers. In this example, the code imports geospatial data representing the location of pre-schools (childcare centres and kindergartens) around Singapore from a KML file. The data is sourced from Singapore Government

4 Checking the Content of A Simple Feature Data Frame

When working with a geospatial data frame like ‘mpsz’ (or any dataset in general), it’s essential to understand its structure and content. The following codes are for checking and understanding the data:

The st_geometry function is used to extract the geometric information (shapes) from the mpsz (Master Plan Subzone Boundary 2014) feature data frame.

st_geometry(mpsz)

Geometry set for 323 features 
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
Projected CRS: SVY21
First 5 geometries:

From the output of the code, it can be summarized that:

The dataset contains 323 features, each representing a geographic entity. The geometry type used is MULTIPOLYGON, indicating that these features consist of multiple connected polygons.
The dimension is XY, implying that the geometry is represented in a two-dimensional space with X and Y coordinates.
The bounding box provides the spatial extent of the dataset which includes xmin (minimum X-coordinate), ymin (minimum Y-coordinate), xmax (maximum X-coordinate), and ymax (maximum Y-coordinate)
Projection Information: The data is projected in the SVY21 coordinate reference system (CRS). SVY21 is a coordinate system used in Singapore for accurate spatial representation.
First 5 Geometries: The output displays the geometries for the first 5 features in the dataset, each represented as a MULTIPOLYGON.

The glimpse function is employed to obtain a quick overview of the structure and content of the ‘mpsz’ data frame, offering insights into its shape, variables and data types.

glimpse(mpsz)

Rows: 323
Columns: 16
$ OBJECTID   <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
$ SUBZONE_NO <int> 1, 1, 3, 8, 3, 7, 9, 2, 13, 7, 12, 6, 1, 5, 1, 1, 3, 2, 2, …
$ SUBZONE_N  <chr> "MARINA SOUTH", "PEARL'S HILL", "BOAT QUAY", "HENDERSON HIL…
$ SUBZONE_C  <chr> "MSSZ01", "OTSZ01", "SRSZ03", "BMSZ08", "BMSZ03", "BMSZ07",…
$ CA_IND     <chr> "Y", "Y", "Y", "N", "N", "N", "N", "Y", "N", "N", "N", "N",…
$ PLN_AREA_N <chr> "MARINA SOUTH", "OUTRAM", "SINGAPORE RIVER", "BUKIT MERAH",…
$ PLN_AREA_C <chr> "MS", "OT", "SR", "BM", "BM", "BM", "BM", "SR", "QT", "QT",…
$ REGION_N   <chr> "CENTRAL REGION", "CENTRAL REGION", "CENTRAL REGION", "CENT…
$ REGION_C   <chr> "CR", "CR", "CR", "CR", "CR", "CR", "CR", "CR", "CR", "CR",…
$ INC_CRC    <chr> "5ED7EB253F99252E", "8C7149B9EB32EEFC", "C35FEFF02B13E0E5",…
$ FMEL_UPD_D <date> 2014-12-05, 2014-12-05, 2014-12-05, 2014-12-05, 2014-12-05…
$ X_ADDR     <dbl> 31595.84, 28679.06, 29654.96, 26782.83, 26201.96, 25358.82,…
$ Y_ADDR     <dbl> 29220.19, 29782.05, 29974.66, 29933.77, 30005.70, 29991.38,…
$ SHAPE_Leng <dbl> 5267.381, 3506.107, 1740.926, 3313.625, 2825.594, 4428.913,…
$ SHAPE_Area <dbl> 1630379.27, 559816.25, 160807.50, 595428.89, 387429.44, 103…
$ geometry   <MULTIPOLYGON [m]> MULTIPOLYGON (((31495.56 30..., MULTIPOLYGON (…

From the output of the code, it can be summarized that the dataset contains 323 row and 16 columns, with various data type including integer (int), characters/string (chr), date, double-precision floating-point/64bit float (dbl), and multipolygon

The head function is utilized to display the initial 5 rows of the ‘mpsz’ data frame, providing a glimpse of its data values. The n=5 parameter specifies the number of rows to be shown (in this case, the first 5 rows).

head(mpsz, n=5)

Simple feature collection with 5 features and 15 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 25867.68 ymin: 28369.47 xmax: 32362.39 ymax: 30435.54
Projected CRS: SVY21
  OBJECTID SUBZONE_NO      SUBZONE_N SUBZONE_C CA_IND      PLN_AREA_N
1        1          1   MARINA SOUTH    MSSZ01      Y    MARINA SOUTH
2        2          1   PEARL'S HILL    OTSZ01      Y          OUTRAM
3        3          3      BOAT QUAY    SRSZ03      Y SINGAPORE RIVER
4        4          8 HENDERSON HILL    BMSZ08      N     BUKIT MERAH
5        5          3        REDHILL    BMSZ03      N     BUKIT MERAH
  PLN_AREA_C       REGION_N REGION_C          INC_CRC FMEL_UPD_D   X_ADDR
1         MS CENTRAL REGION       CR 5ED7EB253F99252E 2014-12-05 31595.84
2         OT CENTRAL REGION       CR 8C7149B9EB32EEFC 2014-12-05 28679.06
3         SR CENTRAL REGION       CR C35FEFF02B13E0E5 2014-12-05 29654.96
4         BM CENTRAL REGION       CR 3775D82C5DDBEFBD 2014-12-05 26782.83
5         BM CENTRAL REGION       CR 85D9ABEF0A40678F 2014-12-05 26201.96
    Y_ADDR SHAPE_Leng SHAPE_Area                       geometry
1 29220.19   5267.381  1630379.3 MULTIPOLYGON (((31495.56 30...
2 29782.05   3506.107   559816.2 MULTIPOLYGON (((29092.28 30...
3 29974.66   1740.926   160807.5 MULTIPOLYGON (((29932.33 29...
4 29933.77   3313.625   595428.9 MULTIPOLYGON (((27131.28 30...
5 30005.70   2825.594   387429.4 MULTIPOLYGON (((26451.03 30...

The output describes the data as a Simple feature collection with 5 features and 15 fields. Note that the features will change in accordance with the numer in the ‘n’ parameter changed. Field represents the number of columns in the dataset. Note that it only count 15 columns in the dataset as opposed to 16 columns in ‘glimpse’ function. It is because of the ‘geometry’ column is not counted as a ‘geometry’ column is not counted as a ‘simple feature’.

5 Visualizing the Geospatial Data on Chart/Plot

In geospatial data science, by looking at the feature information is not enough. We are also interested to visualise the geospatial features. THe following visualization use plot function from sf library. Note that ‘plot()’ function is mean for plotting the geospatial object for quick look. For high cartographic quality plot, other R package such as tmap should be used.

The plot function is used to visualize all features in the ‘mpsz’ dataset. The max.plot parameter limits the display to a maximum of 15 features

plot(mpsz, max.plot = 15)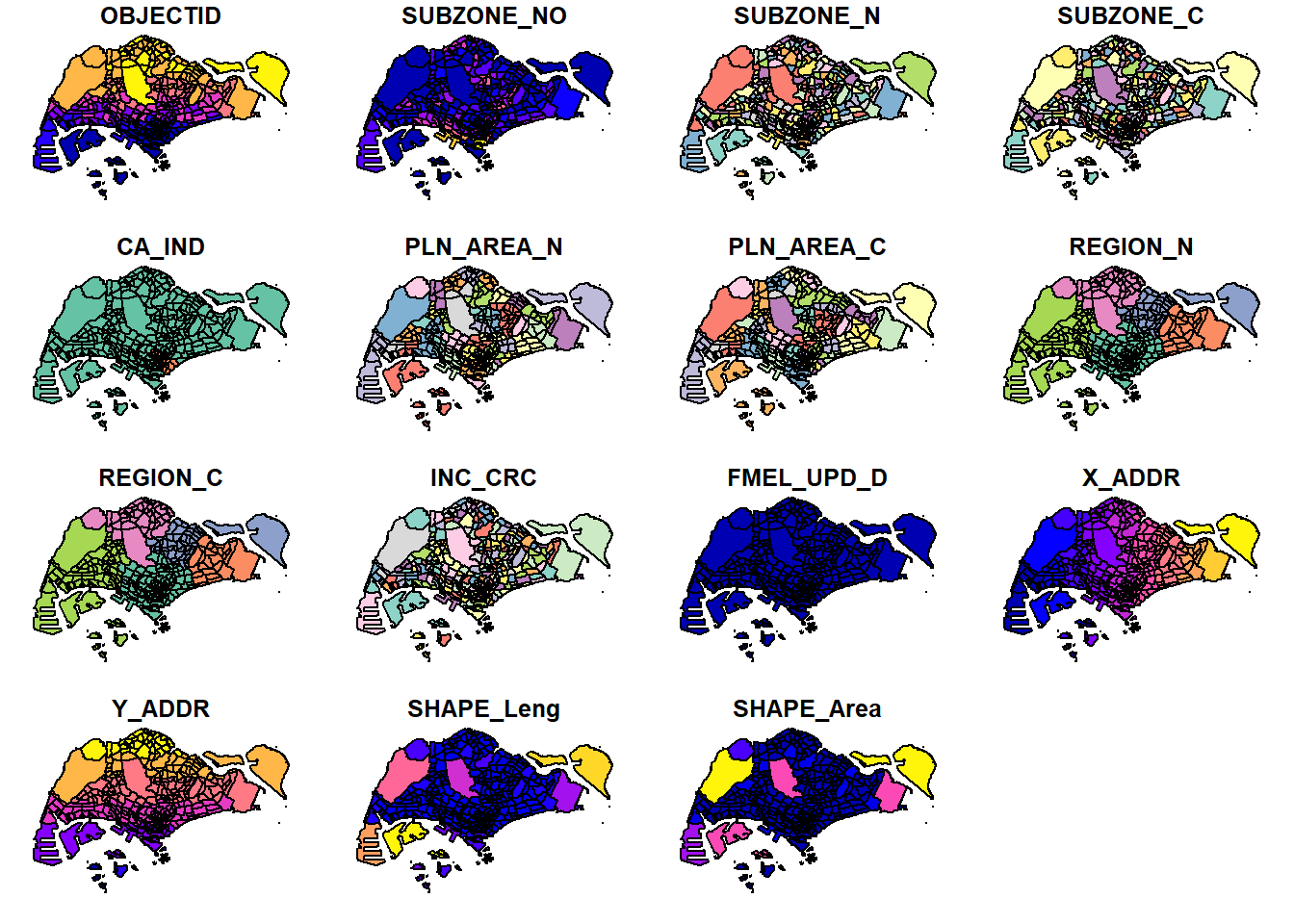

Here, the plot function is applied to display only the geometric shapes from the ‘mpsz’ dataset. The st_geometry function extracts the geometries, and the plot focuses solely on the spatial representation.

plot(st_geometry(mpsz))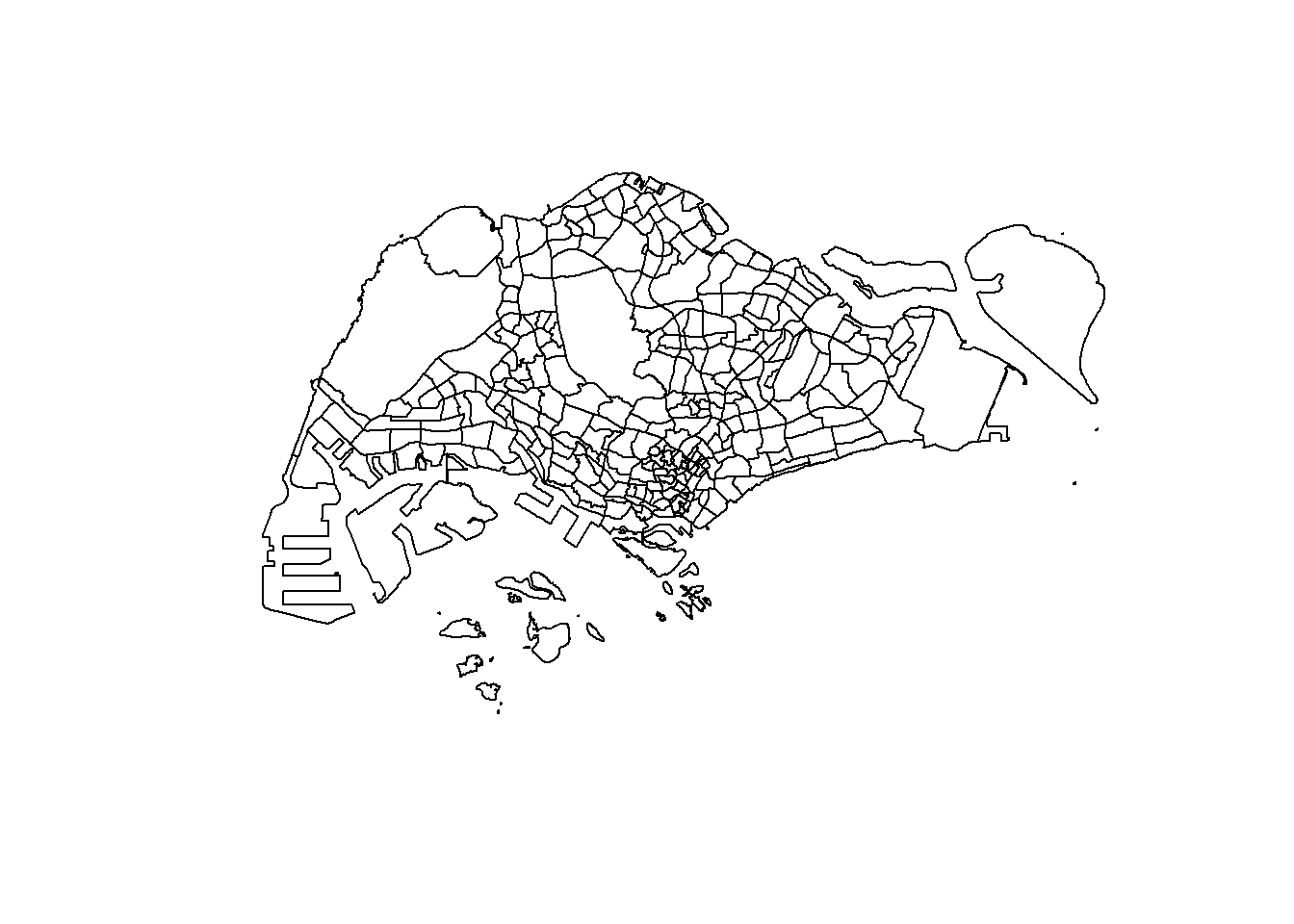

This code utilizes the plot function to visualize features from the ‘mpsz’ dataset based on the attribute “PLN_AREA_N.” The resulting plot highlights spatial distributions based on the specified attribute, providing insights into the geographic distribution of the selected feature.

plot(mpsz["PLN_AREA_N"])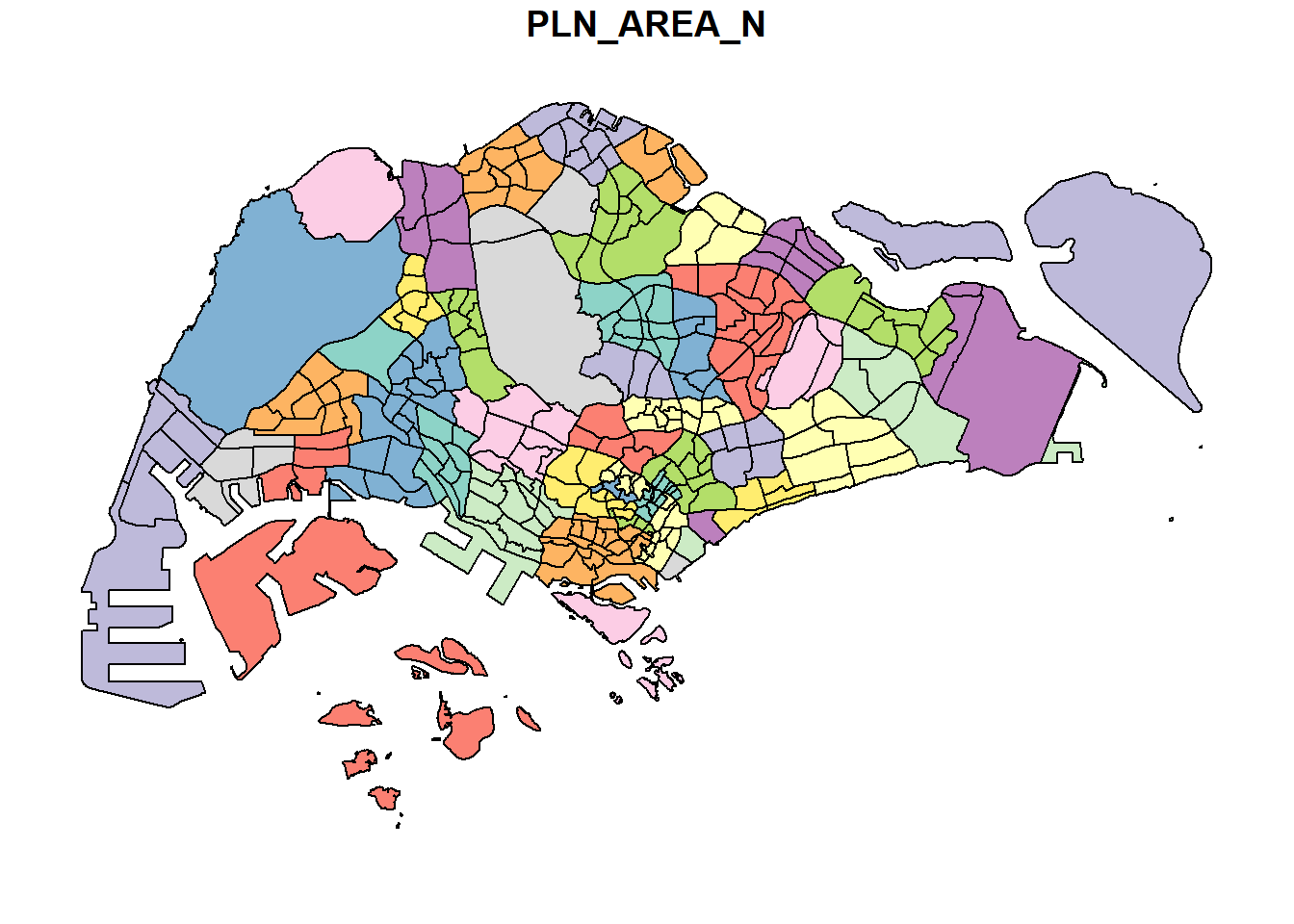

6 Working with Projection

Map projection is an important property of a geospatial data. In order to perform geoprocessing using two geospatial data, we need to ensure that both geospatial data are projected using similar coordinate system. In this section, you will learn how to project a simple feature data frame from one coordinate system to another coordinate system. The technical term of this process is called projection transformation.

6.1 Assigning EPSG code to a simple feature data frame

One of the common issue that can happen during importing geospatial data into R is that the coordinate system of the source data was either missing (such as due to missing .proj for ESRI shapefile) or wrongly assigned during the importing process.

The st_crs is a function to retrieve coordinate reference system from sf or sfc object. In this case, it is used to obtain the current EPSG code of the ‘mpsz’ dataset, providing information about its current coordinate reference system. The EPSG code (European Petroleum Survey Group) is a standardized identifier used to uniquely reference a coordinate reference system.

st_crs(mpsz)

Coordinate Reference System:
  User input: SVY21 
  wkt:
PROJCRS["SVY21",
    BASEGEOGCRS["SVY21[WGS84]",
        DATUM["World Geodetic System 1984",
            ELLIPSOID["WGS 84",6378137,298.257223563,
                LENGTHUNIT["metre",1]],
            ID["EPSG",6326]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["Degree",0.0174532925199433]]],
    CONVERSION["unnamed",
        METHOD["Transverse Mercator",
            ID["EPSG",9807]],
        PARAMETER["Latitude of natural origin",1.36666666666667,
            ANGLEUNIT["Degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",103.833333333333,
            ANGLEUNIT["Degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["Scale factor at natural origin",1,
            SCALEUNIT["unity",1],
            ID["EPSG",8805]],
        PARAMETER["False easting",28001.642,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",38744.572,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["(E)",east,
            ORDER[1],
            LENGTHUNIT["metre",1,
                ID["EPSG",9001]]],
        AXIS["(N)",north,
            ORDER[2],
            LENGTHUNIT["metre",1,
                ID["EPSG",9001]]]]

Although mpsz data frame is projected in svy21 but when we read until the end of the print, it indicates that the EPSG is 9001. This is a wrong EPSG code because the correct EPSG code for svy21 should be 3414. This code assigns the EPSG code 3414 to the ‘mpsz’ dataset, ensuring that it adheres to the SVY21 coordinate reference system (EPSG 3414) for accurate spatial representation.

mpsz3414 <- st_set_crs(mpsz, 3414)

The following code is to re-run st_crs to verify that the correction was successful by displaying the updated EPSG code (EPSG 3414) of the ‘mpsz3414’ dataset.

st_crs(mpsz3414)

Coordinate Reference System:
  User input: EPSG:3414 
  wkt:
PROJCRS["SVY21 / Singapore TM",
    BASEGEOGCRS["SVY21",
        DATUM["SVY21",
            ELLIPSOID["WGS 84",6378137,298.257223563,
                LENGTHUNIT["metre",1]]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["degree",0.0174532925199433]],
        ID["EPSG",4757]],
    CONVERSION["Singapore Transverse Mercator",
        METHOD["Transverse Mercator",
            ID["EPSG",9807]],
        PARAMETER["Latitude of natural origin",1.36666666666667,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",103.833333333333,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["Scale factor at natural origin",1,
            SCALEUNIT["unity",1],
            ID["EPSG",8805]],
        PARAMETER["False easting",28001.642,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",38744.572,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["northing (N)",north,
            ORDER[1],
            LENGTHUNIT["metre",1]],
        AXIS["easting (E)",east,
            ORDER[2],
            LENGTHUNIT["metre",1]],
    USAGE[
        SCOPE["Cadastre, engineering survey, topographic mapping."],
        AREA["Singapore - onshore and offshore."],
        BBOX[1.13,103.59,1.47,104.07]],
    ID["EPSG",3414]]

6.2 Transforming the projection of preschool from wgs84 to svy21

In geospatial analytics, it is very common for us to transform the original data from geographic coordinate system to projected coordinate system. This is because geographic coordinate system is not appropriate if the analysis need to use distance or/and area measurements. This following code utilizes st_transform to convert the projection of the preschool dataset from the WGS84 coordinate system to the SVY21 coordinate system (EPSG 3414). This transformation ensures compatibility with other spatial data in the SVY21 projection.

preschool3414 <- st_transform(preschool, crs = 3414)

7 Importing and Converting an Aspatial Data

In practice, it is not unusual that we will come across data such as listing of Inside Airbnb. We call this kind of data aspatial data. This is because it is not a geospatial data but among the data fields, there are two fields that capture the x- and y-coordinates of the data points. In this section, you will learn how to import an aspatial data into R environment and save it as a tibble data frame. Next, you will convert it into a simple feature data frame.

Importing the aspatial data
Creating a simple feature data frame from an aspatial data frame

Since listings data set is in csv file format, we will use read_csv() of readr package to import listing.csv as shown the code chunk below. The output R object is called listings and it is a tibble data frame.

listings <- read_csv("../data/aspatial/listings.csv")

Displaying the Aspatial Data This code displays the content of the ‘listings’ data frame, providing a preview of its structure and values.

list(listings)

[[1]]
# A tibble: 3,483 × 18
       id name      host_id host_name neighbourhood_group neighbourhood latitude
    <dbl> <chr>       <dbl> <chr>     <chr>               <chr>            <dbl>
 1  71609 Villa in…  367042 Belinda   East Region         Tampines          1.35
 2  71896 Home in …  367042 Belinda   East Region         Tampines          1.35
 3  71903 Home in …  367042 Belinda   East Region         Tampines          1.35
 4 275343 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
 5 275344 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
 6 289234 Home in …  367042 Belinda   East Region         Tampines          1.34
 7 294281 Rental u… 1521514 Elizabeth Central Region      Newton            1.31
 8 324945 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
 9 330095 Rental u… 1439258 Kay       Central Region      Bukit Merah       1.29
10 369141 Place to… 1521514 Elizabeth Central Region      Newton            1.31
# ℹ 3,473 more rows
# ℹ 11 more variables: longitude <dbl>, room_type <chr>, price <dbl>,
#   minimum_nights <dbl>, number_of_reviews <dbl>, last_review <date>,
#   reviews_per_month <dbl>, calculated_host_listings_count <dbl>,
#   availability_365 <dbl>, number_of_reviews_ltm <dbl>, license <chr>

The output reveals that listing tibble data frame consists of 4252 rows and 16 columns. Two useful fields we are going to use in the next phase are latitude and longitude. Note that they are in decimal degree format. As a best guess, we will assume that the data is in wgs84 Geographic Coordinate System.

This code converts the listings data frame into a simple feature data frame named listings_sf. It assigns coordinates and transforms the CRS to SVY21 (EPSG 3414) for accurate spatial representation

listings_sf <- st_as_sf(listings, coords = c("longitude", "latitude"), crs=4326) %>% st_transform(crs = 3414)

Things to learn from the arguments above: - coords argument requires you to provide the column name of the x-coordinates first then followed by the column name of the y-coordinates. - crs argument requires you to provide the coordinates system in epsg format. EPSG: 4326 is wgs84 Geographic Coordinate System and EPSG: 3414 is Singapore SVY21 Projected Coordinate System. You can search for other country’s epsg code by referring to epsg.io. - %>% is used to nest st_transform() to transform the newly created simple feature data frame into svy21 projected coordinates system.

examine the content using glimpse function

glimpse(listings_sf)

Rows: 3,483
Columns: 17
$ id                             <dbl> 71609, 71896, 71903, 275343, 275344, 28…
$ name                           <chr> "Villa in Singapore · ★4.44 · 2 bedroom…
$ host_id                        <dbl> 367042, 367042, 367042, 1439258, 143925…
$ host_name                      <chr> "Belinda", "Belinda", "Belinda", "Kay",…
$ neighbourhood_group            <chr> "East Region", "East Region", "East Reg…
$ neighbourhood                  <chr> "Tampines", "Tampines", "Tampines", "Bu…
$ room_type                      <chr> "Private room", "Private room", "Privat…
$ price                          <dbl> 150, 80, 80, 55, 69, 220, 85, 75, 45, 7…
$ minimum_nights                 <dbl> 92, 92, 92, 60, 60, 92, 92, 60, 60, 92,…
$ number_of_reviews              <dbl> 20, 24, 47, 22, 17, 12, 133, 18, 6, 81,…
$ last_review                    <date> 2020-01-17, 2019-10-13, 2020-01-09, 20…
$ reviews_per_month              <dbl> 0.14, 0.16, 0.31, 0.17, 0.12, 0.09, 0.9…
$ calculated_host_listings_count <dbl> 5, 5, 5, 52, 52, 5, 7, 52, 52, 7, 7, 1,…
$ availability_365               <dbl> 89, 89, 89, 275, 274, 89, 365, 365, 365…
$ number_of_reviews_ltm          <dbl> 0, 0, 0, 0, 3, 0, 0, 1, 3, 0, 0, 0, 0, …
$ license                        <chr> NA, NA, NA, "S0399", "S0399", NA, NA, "…
$ geometry                       <POINT [m]> POINT (41972.5 36390.05), POINT (…

Table above shows the content of listing_sf. Notice that a new column called geometry has been added into the data frame. On the other hand, the longitude and latitude columns have been dropped from the data frame.

8 Geoprocessing with sf package

Besides providing functions to handling (i.e. importing, exporting, assigning projection, transforming projection etc) geospatial data, sf package also offers a wide range of geoprocessing (also known as GIS analysis) functions. In this section, you will learn how to perform two commonly used geoprocessing functions, namely buffering and point in polygon count.

Buffering
Point-in-polygon count

The scenario: The authority is planning to upgrade the exiting cycling path. To do so, they need to acquire 5 metres of reserved land on the both sides of the current cycling path. You are tasked to

The solution: determine the extend of the land need to be acquired and their total area. This code calculates 5-meter buffers around cycling paths and stores the result in the ‘buffer_cycling’ dataset.

buffer_cycling <- st_buffer(cyclingpath, dist=5, nQuadSegs = 30)

calculate the area of buffers The code adds a new column, ‘AREA,’ to the ‘buffer_cycling’ dataset, containing the calculated area of each buffer.

buffer_cycling$AREA <- st_area(buffer_cycling)

derive the total land involved

sum(buffer_cycling$AREA)

1774367 [m^2]

The scenario A pre-school service group want to find out the numbers of pre-schools in each Planning Subzone.

** The solution: The code counts the number of pre-schools within each Planning Subzone using the st_intersects() function and updates the ‘PreSch Count’ column in the ‘mpsz3414’ dataset. Next, length() of Base R is used to calculate numbers of pre-schools that fall inside each planning subzone.

mpsz3414$'PreSch Count'<- lengths(st_intersects(mpsz3414, preschool3414))

checking the summary statistics

summary(mpsz3414$`PreSch Count`)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    0.00    4.00    7.09   10.00   72.00

checking the subzone with most number of pre-school To list the planning subzone with the most number of pre-school, the top_n() of dplyr package is used as shown in the code chunk below.

top_n(mpsz3414, 1, `PreSch Count`)

Simple feature collection with 1 feature and 16 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 39655.33 ymin: 35966 xmax: 42940.57 ymax: 38622.37
Projected CRS: SVY21 / Singapore TM
  OBJECTID SUBZONE_NO     SUBZONE_N SUBZONE_C CA_IND PLN_AREA_N PLN_AREA_C
1      189          2 TAMPINES EAST    TMSZ02      N   TAMPINES         TM
     REGION_N REGION_C          INC_CRC FMEL_UPD_D   X_ADDR   Y_ADDR SHAPE_Leng
1 EAST REGION       ER 21658EAAF84F4D8D 2014-12-05 41122.55 37392.39   10180.62
  SHAPE_Area                       geometry PreSch Count
1    4339824 MULTIPOLYGON (((42196.76 38...           72

calculating the density of pre-school by planning subzone This code calculates the area of each Planning Subzone and adds a new column, ‘Area,’ to the ‘mpsz3414’ dataset.

mpsz3414$Area <- mpsz3414 %>%
  st_area()

compute pre-schoold density The code computes the density of pre-schools per square kilometer for each Planning Subzone, providing a measure of the concentration of educational facilities in different areas.

mpsz3414 <- mpsz3414 %>%
  mutate(`PreSch Density` = `PreSch Count`/Area * 1000000)

9 Exploratory Data Analysis (EDA)

In practice, many geospatial analytics start with Exploratory Data Analysis. In this section, you will learn how to use appropriate ggplot2 functions to create functional and yet truthful statistical graphs for EDA purposes.

The histogram visualizes the distribution of pre-school density across different Planning Subzones, providing insights into the variation and concentration of pre-schools in Singapore.

hist(mpsz3414$`PreSch Density`)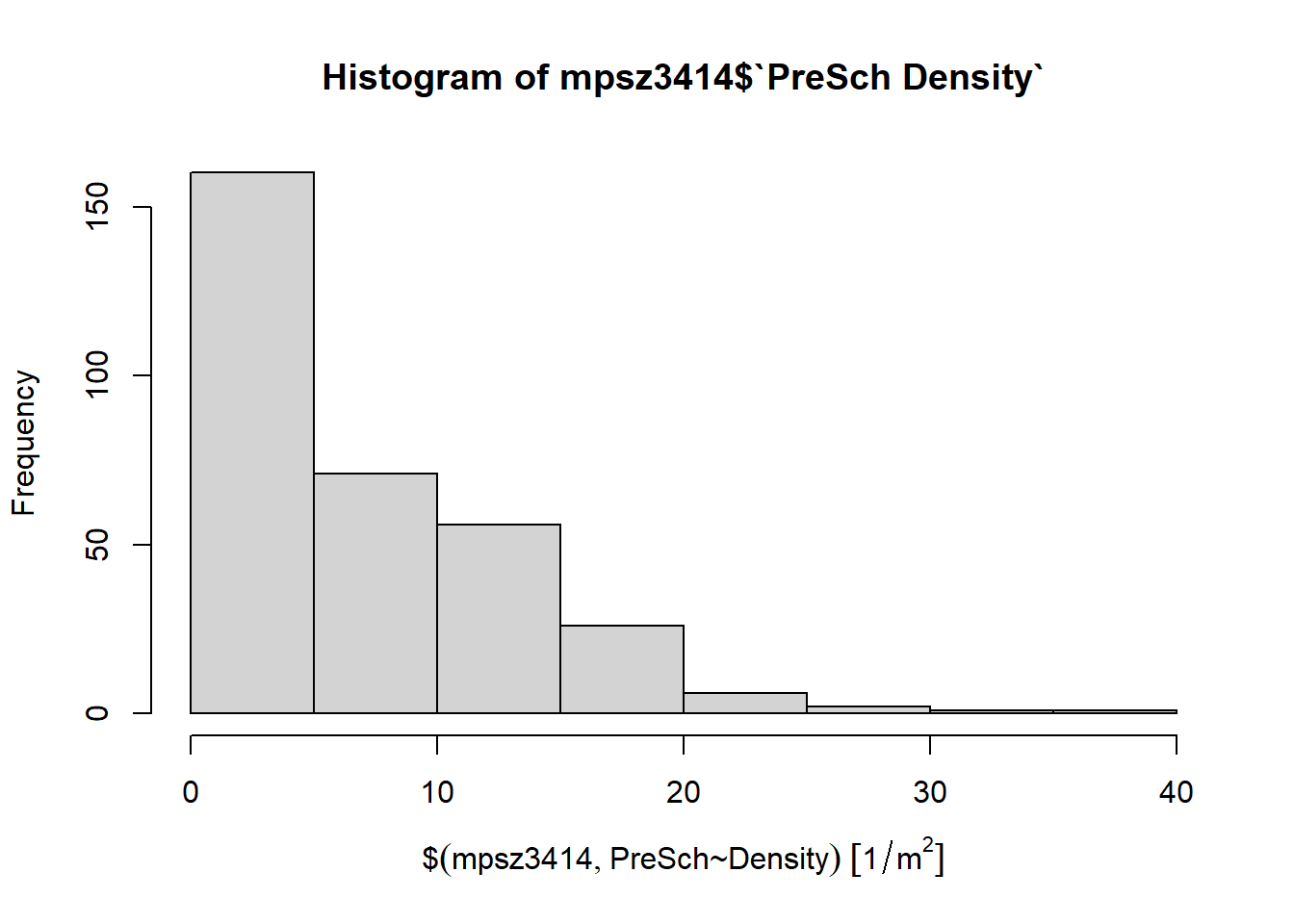

This GG Plot-generated histogram offers a more detailed view of pre-school density, allowing for a nuanced exploration of the distribution in Planning Subzones. The chart provides additional context on the prevalence of single pre-school areas versus those with higher concentrations.

Code

ggplot(data=mpsz3414, 
       aes(x= as.numeric(`PreSch Density`)))+
  geom_histogram(bins=20, 
                 color="black", 
                 fill="light blue") +
  labs(title = "Are pre-school even distributed in Singapore?",
       subtitle= "There are many planning sub-zones with a single pre-school, on the other hand, \nthere are two planning sub-zones with at least 20 pre-schools",
      x = "Pre-school density (per km sq)",
      y = "Frequency")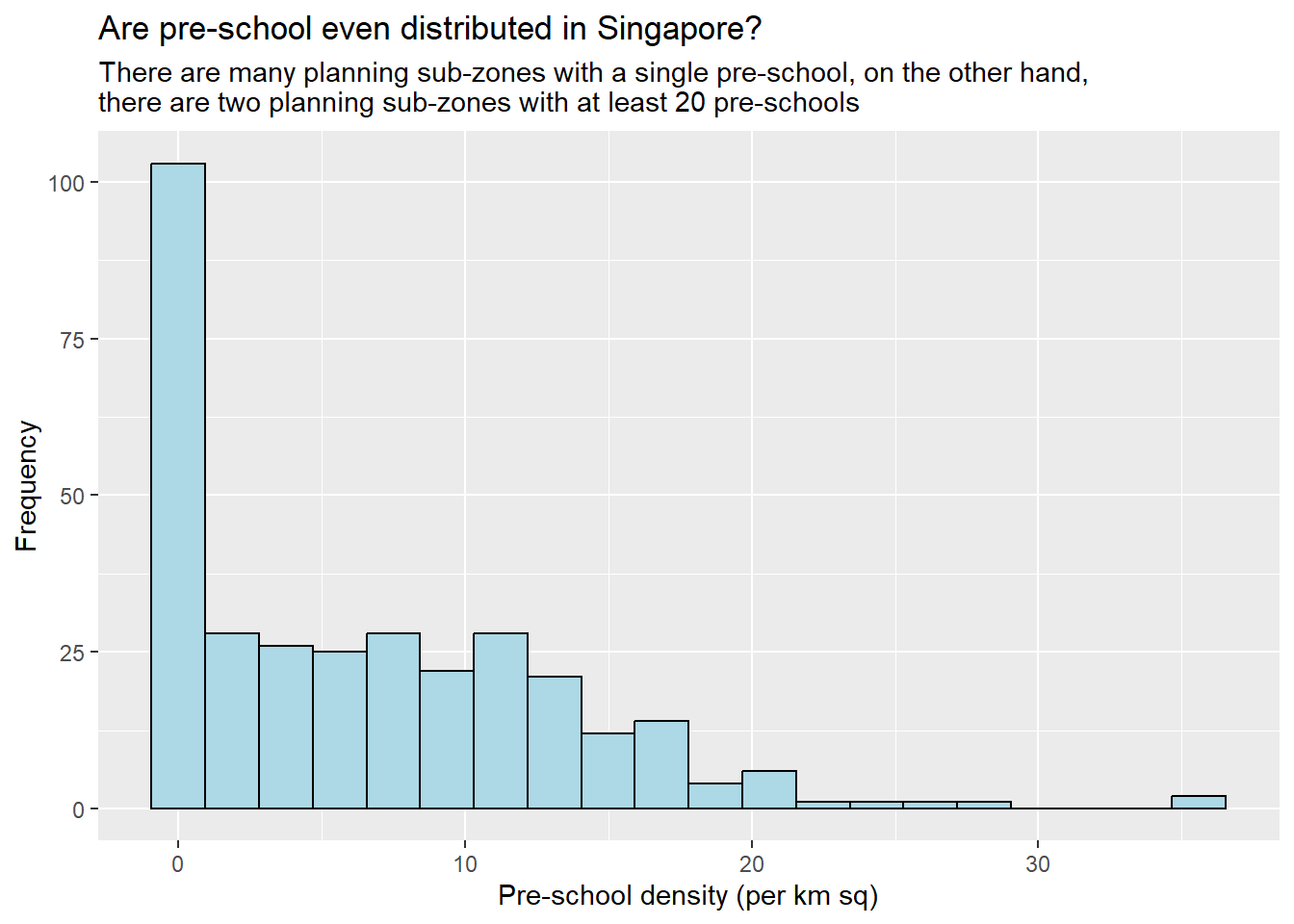

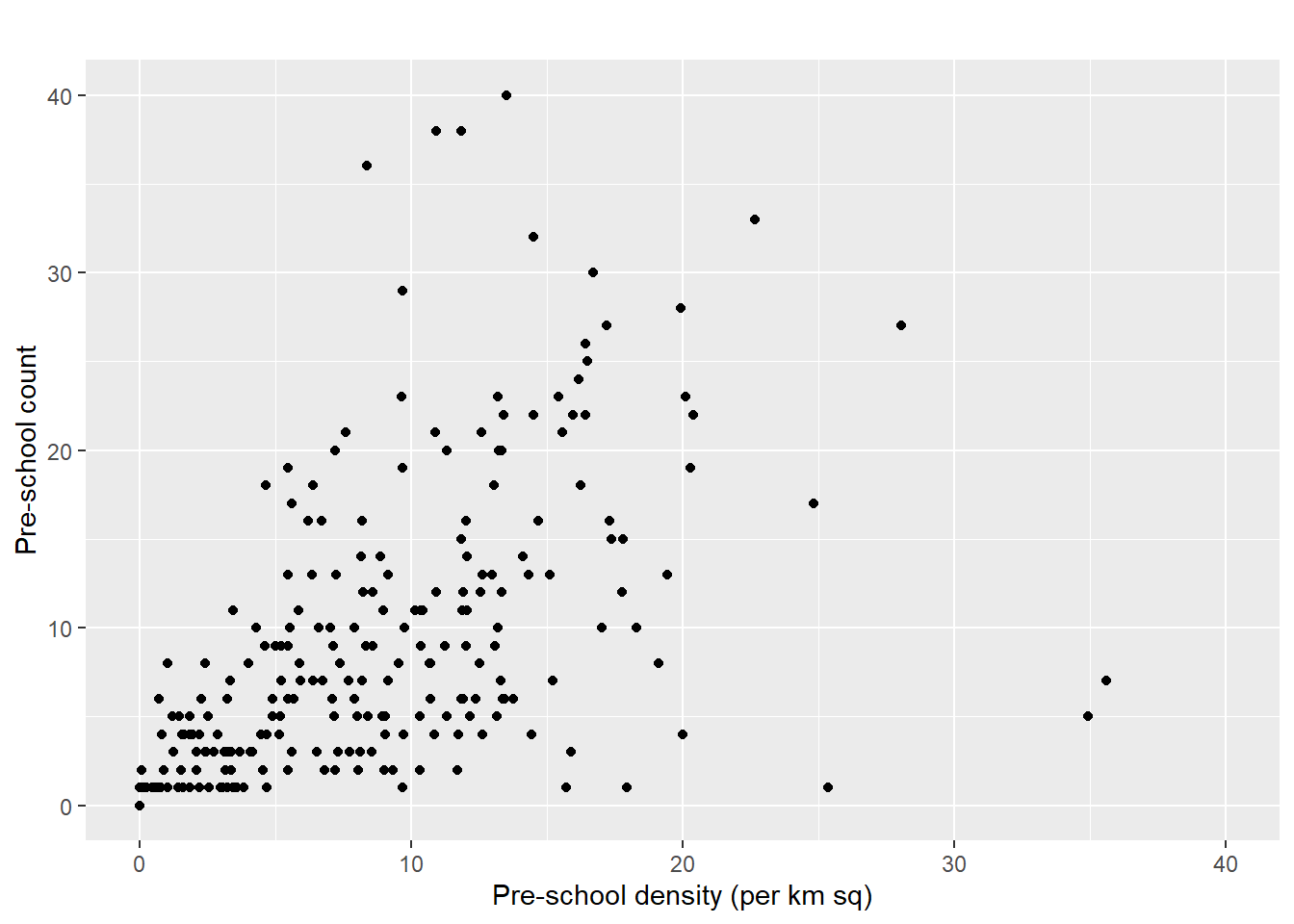
This scatterplot employs GG Plot to illustrate the relationship between pre-school density and count in different Planning Subzones. It helps identify patterns, clusters, or outliers, facilitating a comprehensive understanding of the distribution and concentration of pre-schools. The chart is limited to a specific range for clarity in visualization.

Code

ggplot(data=mpsz3414, 
       aes(y = `PreSch Count`, 
           x= as.numeric(`PreSch Density`)))+
  geom_point(color="black", 
             fill="light blue") +
  xlim(0, 40) +
  ylim(0, 40) +
  labs(title = "",
      x = "Pre-school density (per km sq)",
      y = "Pre-school count")